
【题目】点![]() 在数轴上表示的数
在数轴上表示的数![]() 满足
满足![]() ,且多项式
,且多项式![]() 是五次四项式.
是五次四项式.
(1)![]() 的值为____ ____,
的值为____ ____,![]() 的值为___ ____,
的值为___ ____,![]() 的值为____ ____;
的值为____ ____;
(2)已知点![]() 、点
、点![]() 是数轴上的两个动点,点
是数轴上的两个动点,点![]() 从点
从点![]() 出发,以
出发,以![]() 个单位/秒的速度向右运动,同时点
个单位/秒的速度向右运动,同时点![]() 从点
从点![]() 出发,以
出发,以![]() 个单位/秒的速度向左运动:
个单位/秒的速度向左运动:
① 若点![]() 和点
和点![]() 经过
经过![]() 秒后在数轴上的点
秒后在数轴上的点![]() 处相遇,求出
处相遇,求出![]() 的值和点
的值和点![]() 所表示的数;
所表示的数;
② 若点![]() 运动到点
运动到点![]() 处,动点
处,动点![]() 再出发,则
再出发,则![]() 运动几秒后这两点之间的距离为5个单位?
运动几秒后这两点之间的距离为5个单位?
【答案】(1) -6;-3;24;(2)①3;3;②3.2秒或4.2秒.
【解析】
试题(1)由非负数的性质可得b+3=0,c-24=0,由多项式为五次四项式得![]() ,解得a、b和c的值;
,解得a、b和c的值;
(2)①利用点P、Q所走的路程=AC列出方程;
②此题需要分类讨论:相遇前和相遇后两种情况下PQ=5所需要的时间.
试题解析:(1) 由题意得,b+3=0,c-24=0,![]() ,-a≠0,
,-a≠0,
解得b=-3,c=24,a=-6,
故答案是:-6;-2;24;
(2)①依题意得 3t+7t=|-6-24|=30,
解得 t=3,
则3t=9,
所以-6+9=3,
所以出t的值是3和点D所表示的数是3;
②设点P运动x秒后,P、Q两点间的距离是5.
当点P在点Q的左边时,3x+5+7(x-1)=30,
解得 x=3.2.
当点P在点Q的右边时,3x-5+7(x-1)=30,
解得 x=4.2.
综上所述,当点P运动3.2秒或4.2秒后,这两点之间的距离为5个单位.


科目:初中数学 来源: 题型:
【题目】用A、B两种机器人搬运大米,A型机器人比B型机器人每小时多搬运20袋大米,A型机器人搬运700袋大米与B型机器人搬运500袋大米所用时间相等.求A、B型机器人每小时分别搬运多少袋大米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,D为BC边上一个动点(D与B、C均不重合),AD=AE,∠DAE=60°,连接CE.
(1)求证:△ABD≌△ACE;
(2)求证:CE平分∠ACF;
(3)若AB=2,当四边形ADCE的周长取最小值时,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个组合烟花的横截面,其中16个圆的半径相同,点A、B、C、D分别是四个角上的圆的圆心,且四边形ABCD为正方形.若圆的半径为r,组合烟花的高为h,则组合烟花侧面包装纸的面积至少需要(接缝面积不计)( ) 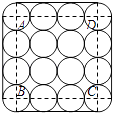
A.26πrh
B.24rh+πrh
C.12rh+2πrh
D.24rh+2πrh
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】丁丁想在一个矩形材料中剪出如图阴影所示的梯形,作为要制作的风筝的一个翅膀.请你根据图中的数据帮丁丁计算出BE、CD的长度(精确到个位, ![]() ≈1.7).
≈1.7). 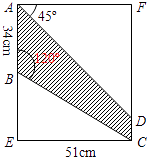
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】央视热播节目“朗读者”激发了学生的阅读兴趣.某校为满足学生的阅读需求,欲购进一批学生喜欢的图书,学校组织学生会成员随机抽取部分学生进行问卷调查,被调查学生须从“文史类、社科类、小说类、生活类”中选择自己喜欢的一类,根据调查结果绘制了统计图(未完成),请根据图中信息,解答下列问题:
(1)此次共调查了 名学生;
(2)将条形统计图补充完整;
(3)图2中“小说类”所在扇形的圆心角为 度;
(4)若该校共有学生2500人,估计该校喜欢“社科类”书籍的学生人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,AB=5cm,BC=3cm,若点P从点A出发,以每秒2cm的速度沿折线A﹣C﹣B﹣A运动,设运动时间为t秒(t>0).

(1)若点P在AC上,且满足PA=PB时,求出此时t的值;
(2)若点P恰好在∠BAC的角平分线上,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DE是△ABC的中位线,F是DE的中点,CF的延长线交AB于点G,若△CEF的面积为12cm2,则S△DGF的值为( )

A.4cm2 B.6cm2 C.8cm2 D.9cm2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com