Question

20．如图，△ABC是等腰直角三角形，∠A=90°，BC=4，点P是△BAC边上一动点，沿B→A→C的路径移动，过P点作PD⊥BC于D点，BD=x，△BDP的面积为y，则下列能大致反映y与x的函数关系的图象的是（　　）

• A．
• B．
• C．
• D．

Answer 1

分析 过A点作AH⊥BC于H，利用等腰直角三角形的性质得到∠B=∠C=45°，BH=CH=AH=$\frac{1}{2}$BC=2，分类讨论：当0≤x≤2时，如图1，易得PD=BD=x，根据三角形面积公式得到y=$\frac{1}{2}$x²；当2＜x≤4时，如图2，易得PD=CD=4-x，根据三角形面积公式得到y=-$\frac{1}{2}$x²+2x，于是可判断当0≤x≤2时，y与x的函数关系的图象为开口向上的抛物线的一部分，当2＜x≤4时，y与x的函数关系的图象为开口向下的抛物线的一部分，然后利用此特征可对四个选项进行判断．

解答 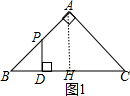解：过A点作AH⊥BC于H，
∵△ABC是等腰直角三角形，
∴∠B=∠C=45°，BH=CH=AH=$\frac{1}{2}$BC=2，
当0≤x≤2时，如图1，
∵∠B=45°，
∴PD=BD=x，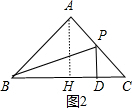
∴y=$\frac{1}{2}$•x•x=$\frac{1}{2}$x²；
当2＜x≤4时，如图2，
∵∠C=45°，
∴PD=CD=4-x，
∴y=$\frac{1}{2}$•（4-x）•x=-$\frac{1}{2}$x²+2x，
故选A．

点评 本题考查了动点问题的函数图象：函数图象是典型的数形结合，图象应用信息广泛，通过看图获取信息，不仅可以解决生活中的实际问题，还可以提高分析问题、解决问题的能力．解决本题的关键是利用分类讨论的思想求出y与x的函数关系式．