
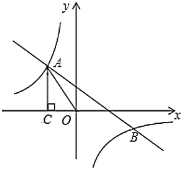
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于第二、四象限内的点
的图象交于第二、四象限内的点![]() 和点
和点![]() .过点
.过点![]() 作
作![]() 轴的垂线,垂足为点
轴的垂线,垂足为点![]() ,
,![]() 的面积为4.若在
的面积为4.若在![]() 轴上取点
轴上取点![]() ,则当
,则当![]() 取得最大值时,点
取得最大值时,点![]() 的坐标为______.
的坐标为______.
【答案】![]()
【解析】
由△AOC的面积为4,可求出a的值,确定反比例函数的关系式,把点B坐标代入反比例函数解析式可求b的值.作点B关于x轴的对称点B′,则直线AB′与x轴交点就是所求的点P,求出直线与x轴的交点坐标即可.
解:∵点A(a,4),
∴AC=4,
∵S△AOC=4,即![]() OCAC=4,
OCAC=4,
∴OC=2,
∵点A(a,4)在第二象限,
∴a=-2,A(-2,4),
将A(-2,4)代入y=![]() 得:k=-8,
得:k=-8,
∴反比例函数的关系式为:y=![]() ,
,
把B(8,b)代入得:b=-1,
∴B(8,-1)
因此a=-2,b=-1;
如图,作点B关于x轴的对称点B′,直线AB′与x轴交于P,
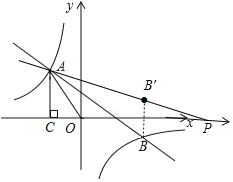
此时PA-PB最大(PA-PB=PA-PB′≤AB′,共线时差最大).
∵B(8,-1)
∴B′(8,1)
设直线AP的关系式为y=kx+b,将 A(-2,4),B′(8,1)代入得:
![]() ,
,
解得:k=![]() ,b=
,b=![]() ,
,
∴直线AP的关系式为![]() ,
,
当y=0时,即![]() =0,
=0,
解得x=![]() ,
,
∴P(![]() ,0).
,0).
故答案为:(![]() ,0).
,0).


科目:初中数学 来源: 题型:
【题目】国内猪肉价格不断上涨,已知今年10月的猪肉价格比今年年初上涨了80%,李奶奶10月在某超市购买1千克猪肉花了72元钱.
(1)今年年初猪肉的价格为每千克多少元?
(2)某超市将进货价为每千克55元的猪肉按10月价格出售,平均一天能销售出100千克,随着国家对猪肉价格的调控,超市发现猪肉的售价每千克下降1元,其日销售量就增加10千克,超市为了实现销售猪肉每天有1800元的利润,并且尽可能让顾客得到实惠,猪肉的售价应该下降多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知如图所示的抛物线顶点![]() 的坐标为
的坐标为![]() ,且过点
,且过点![]() .
.
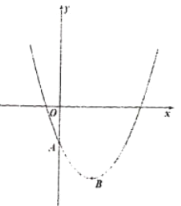
(1)求该抛物线的解析式;
(2)若点![]() 为抛物线对称轴右侧、
为抛物线对称轴右侧、![]() 轴下方一点,当
轴下方一点,当![]() 时,求直线
时,求直线![]() 的解析式;
的解析式;
(3)平移(1)中的抛物线,记平移后抛物线的顶点为![]() ,顶点
,顶点![]() 在直线
在直线![]() 上滑动,且平移后的抛物线与直线
上滑动,且平移后的抛物线与直线![]() 交于另一点
交于另一点![]() ,若点
,若点![]() 为平移前(1)中抛物线上的点,则当以
为平移前(1)中抛物线上的点,则当以![]() 、
、![]() 、
、![]() 三点为顶点的三角形是等腰直角三角形时,求出所有符合条件的点
三点为顶点的三角形是等腰直角三角形时,求出所有符合条件的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
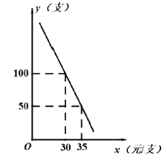
【题目】某网店专售一款电动牙刷,其成本为 20 元/支,销售中发现该商品每天的销售量 ![]() (支)与销售单价
(支)与销售单价 ![]() (元/支)之间存在如图所示的关系.
(元/支)之间存在如图所示的关系.
(1)求出 ![]() 与
与 ![]() 的函数关系式(不需要写出自变量取值范围);
的函数关系式(不需要写出自变量取值范围);
(2)该款电动牙刷销售单价定为多少元时,每天销售利润最大?最大利润是多少元?
(3)近期武汉爆发了“新型冠状病毒”疫情,该网店店主决定从每天获得的利润中抽出 200元捐赠给武汉,为了保证捐款后每天剩余利润不低于 550 元,试确定该款电动牙刷销售单价![]() 的取值范围?
的取值范围?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店准备购进![]() 两种商品,
两种商品,![]() 种商品毎件的进价比
种商品毎件的进价比![]() 种商品每件的进价多20元,用3000元购进
种商品每件的进价多20元,用3000元购进![]() 种商品和用1800元购进
种商品和用1800元购进![]() 种商品的数量相同.商店将
种商品的数量相同.商店将![]() 种商品每件的售价定为80元,
种商品每件的售价定为80元,![]() 种商品每件的售价定为45元.
种商品每件的售价定为45元.
(1)![]() 种商品每件的进价和
种商品每件的进价和![]() 种商品每件的进价各是多少元?
种商品每件的进价各是多少元?
(2)商店计划用不超过1560元的资金购进![]() 两种商品共40件,其中
两种商品共40件,其中![]() 种商品的数量不低于
种商品的数量不低于![]() 种商品数量的一半,该商店有几种进货方案?
种商品数量的一半,该商店有几种进货方案?
(3)端午节期间,商店开展优惠促销活动,决定对每件![]() 种商品售价优惠
种商品售价优惠![]() (
(![]() )元,
)元,![]() 种商品售价不变,在(2)条件下,请设计出销售这40件商品获得总利润最大的进货方案.
种商品售价不变,在(2)条件下,请设计出销售这40件商品获得总利润最大的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某黄瓜种植基地配置了新的滴灌系统,系统启动后,土壤的湿度![]() 与系统运行时间
与系统运行时间![]() (天)满足一次函数关系;当土壤湿度指数到90时系统自动停止工作,随后土壤的湿度开始下降,此过程中土壤的湿度
(天)满足一次函数关系;当土壤湿度指数到90时系统自动停止工作,随后土壤的湿度开始下降,此过程中土壤的湿度![]() 与时间
与时间![]() (天)成反比例关系;当土壤的湿度降为60时,滴灌系统又开始工作.根据图中提供的函数图象,解答下列问题.
(天)成反比例关系;当土壤的湿度降为60时,滴灌系统又开始工作.根据图中提供的函数图象,解答下列问题.
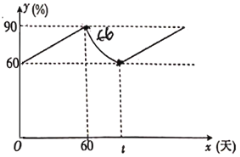
(1)当![]() 时,求空气湿度指数
时,求空气湿度指数![]() 与系统运行时间
与系统运行时间![]() (天)之间的函数解析式.
(天)之间的函数解析式.
(2)求![]() 的值.
的值.
(3)在挂果期间,湿度在![]() 之间最适宜.如果此滴灌系统不做其他设置,那么在一轮工作过程中有多长时间是最适合果实生长的?
之间最适宜.如果此滴灌系统不做其他设置,那么在一轮工作过程中有多长时间是最适合果实生长的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]()
![]() 当抛物线的顶点在
当抛物线的顶点在![]() 轴上时,求该抛物线的解析式;
轴上时,求该抛物线的解析式;
![]() 不论
不论![]() 取何值时,抛物线的顶点始终在一条直线上,求该直线的解析式;
取何值时,抛物线的顶点始终在一条直线上,求该直线的解析式;
![]() 若有两点
若有两点![]() ,
,![]() ,且该抛物线与线段
,且该抛物线与线段![]() 始终有交点,请直接写出
始终有交点,请直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人分别从A,B两地同时出发,匀速相向而行.甲的速度大于乙的速度,甲到达B地后,乙继续前行.设出发x h后,两人相距y km,图中折线表示从两人出发至乙到达A地的过程中y与x之间的函数关系.
根据图中信息,求:
(1)点Q的坐标,并说明它的实际意义;
(2)甲、乙两人的速度.
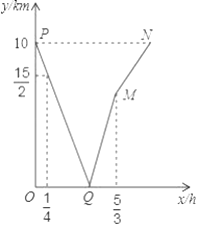
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com