练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    5．如图所示，直线y=kx+b（k≠0）与x轴交于点（-5，0），则关于x的方程kx+b=0的解为x=（　　）
    A．-5B．-4C．0D．1

    分析 利用x=-5时，函数y=kx+b的函数值为0可判断关于x的方程kx+b=0的解．

    解答 解：∵直线y=kx+b（k≠0）与x轴交于点（-5，0），
    ∴关于x的方程kx+b=0的解为x=-5．
    故选A．

    点评 本题考查了一次函数与一元一次方程：利用图象法求出相应一元一次方程的解．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

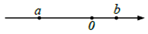    15．有理数a，b在数轴上的位置如图所示，在下列结论中：①ab＜0；②a+b＞0；③a3＞b2；④（a-b）3＜0；⑤a＜-b＜b＜-a；⑥|b-a|-|a|=b?．正确的结论有（　　）
    A．2个B．3个C．4个D．5个

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．若x、y为实数，且y=$\sqrt{x-2}$+$\sqrt{2-x}$+3，求yx的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

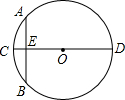    13．“圆材埋壁”是我国古代著名的数学著作《九章算术》中的一个问题，“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问锯几何？”用现代的数学语言表述是：“如图，CD为⊙O的直径，弦AB⊥CD垂足为E，CE=1寸，AB=10寸，求直径CD的长”，依题意，CD长为（　　）
    A．12寸B．13寸C．24寸D．26寸

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．已知方程2xm-1-3=0是关于x的一元一次方程，则m的值是2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．阅读解题过程，回答问题．
    如图，OC在∠AOB内，∠AOB和∠COD都是直角，且∠BOC=30°，求∠AOD的度数．
    解：过O点作射线OM，使点M，O，A在同一直线上．
    因为∠MOD+∠BOD=90°，∠BOC+∠BOD=90°，
    所以∠BOC=∠MOD，
    所以∠AOD=180°-∠BOC=180°-30°=150°
    （1）如果∠BOC=60°，那么∠AOD等于多少度？如果∠BOC=n°，那么∠AOD等于多少度？
    （2）如果∠AOB=∠DOC=x°，∠AOD=y°，求∠BOC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

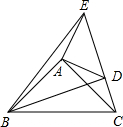    17．已知：如图在△ABC，△ADE中，∠BAC=∠DAE=90°，AB=AC，AD=AE，点C，D，E三点在同一条直线上，连接BD，BE．以下四个结论：①BD=CE；②BD⊥CE；③∠ACE+∠DBC=45°；④BE2=2（AD2+AB2）-CD2，其中结论正确的个数是（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．已知双曲线y=$\frac{k}{x}$经过点（-2，1），则k的值等于（　　）
    A．1B．-1C．2D．-2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

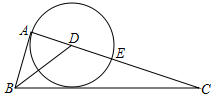    15．如图，在Rt△ABC中，∠BAC=90°，BD是角平分线，以点D为圆心，DA为半径的⊙D与AC相交于点E
    （1）求证：BC是⊙D的切线；
    （2）若AB=5，BC=13，求CE的长．

    查看答案和解析>>

    同步练习册答案