
【题目】如图所示,太阳光线AC和AC是平行的,同一时刻两个建筑物在太阳下的影子一样长,那么建筑物是否一样高?请说明理由.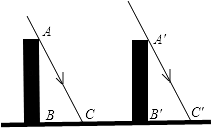
【答案】解:建筑物一样高.
证明:∵AB⊥BC,A′B′⊥B′C′,
∴∠ABC=∠A′B′C′=90°,
∵AC∥A′C′,
∴∠ACB=∠A′C′B′,
在△ABC和△A′B′C′中,![]()
![]()
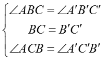 ,
,
∴△ABC≌△A′B′C′(ASA)
∴AB=A′B′.
即建筑物一样高.
【解析】根据已知同一时刻两个建筑物在太阳下的影子一样长,即可得出BC=B′C′,在直角三角形中,可考虑AAS证明三角形全等,从而推出线段相等.
【考点精析】掌握平行线的性质和平行投影是解答本题的根本,需要知道两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;太阳光线可以看成是平行光线,平行光线所形成的投影称为平行投影;作物体的平行投影:由于平行投影的光线是平行的,而物体的顶端与影子的顶端确定的直线就是光线,故根据另一物体的顶端可作出其影子.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,半径为1个单位的圆片上有一点Q与数轴上的原点重合(提示:圆的周长C=2πr,本题中π的取值为3.14)
(1)把圆片沿数轴向右滚动1周,点Q到达数轴上点A的位置,点A表示的数是;
(2)圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:+2,﹣1,﹣5,+4,+3,﹣2
①第几次滚动后,Q点距离原点最近?第几次滚动后,Q点距离原点最远?
②当圆片结束运动时,Q点运动的路程共有多少?此时点Q所表示的数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CE=2DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG∥CF;⑤S△FGC=3.6.其中正确结论的个数是( )
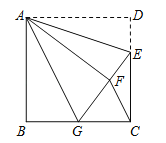
A.2 B.3 C.4 D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,已知△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且B点和C点在AE的异侧,BD⊥AE于D点,CE⊥AE与E点.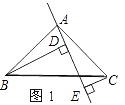
(1)求证:BD=DE+CE
(2)若直线AE绕点A旋转到图2所示的位置时(BD<CE)其余条件不变,问BD 与DE,CE的关系如何?请予以证明.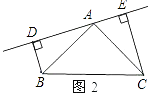
(3)若直线AE绕点A旋转到图3所示的位置时(BD>CE)其余条件不变,问BD 与DE,CE的关系如何?直接写出结果,不需证明.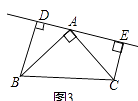
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按下面的程序计算:
当输入 ![]() 时,输出结果是299;当输入
时,输出结果是299;当输入 ![]() 时,输出结果是466;如果输入
时,输出结果是466;如果输入 ![]() 的值是正整数,输出结果是257,那么满足条件的
的值是正整数,输出结果是257,那么满足条件的 ![]() 的值最多有( )
的值最多有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成,硬纸板如图两种方法裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面。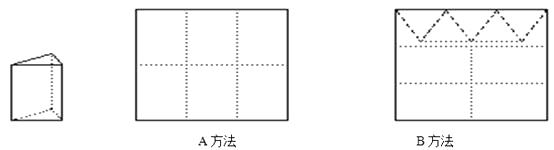
现有38张硬纸板,裁剪时x张用A方法,其余用B方法。
(1)用x的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com