
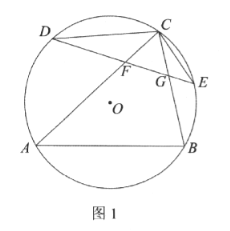
【题目】如图1,![]() 内接于
内接于![]() 分别是
分别是![]() 和
和![]() 所对弧的中点,弦
所对弧的中点,弦![]() 分别交
分别交![]() 于点
于点![]() ,连结
,连结![]()
(1)求证:![]() 是等边三角形.
是等边三角形.
(2)若![]()
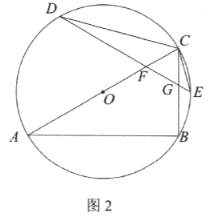
①如图2,当![]() 为
为![]() 的直径时,求
的直径时,求![]() 的长.
的长.
②当![]() 将
将![]() 的面积分成了
的面积分成了![]() 的两部分时,求
的两部分时,求![]() 的长.
的长.
(3)连结![]() 交
交![]() 于点
于点![]() ,若
,若![]() :则
:则![]() 的值为_______. (请直接写出答案)
的值为_______. (请直接写出答案)
【答案】(1)见解析;(2)①8;②![]() 或
或![]() ;(3)
;(3)![]()
【解析】
(1)利用弧的关系证得![]() ,
,![]() ,利用三角形外角的性质证得∠CFG=60°,从而证得
,利用三角形外角的性质证得∠CFG=60°,从而证得![]() 是等边三角形;
是等边三角形;
(2)①连结OD,利用![]() 求得直径AC的长,得到半径OD=
求得直径AC的长,得到半径OD=![]() ,证得∠DOC=90°,在Rt
,证得∠DOC=90°,在Rt![]() 中,再利用
中,再利用![]() 即可求解;
即可求解;
②利用弧的关系![]() =120°=
=120°=![]() ,证得DE=AB=12,分DF:FG=2:1或DF:FG=1:2两种情况讨论,证得△DCF△CEG,利用对应边成比例分别计算即可求解;
,证得DE=AB=12,分DF:FG=2:1或DF:FG=1:2两种情况讨论,证得△DCF△CEG,利用对应边成比例分别计算即可求解;
(3)作出如图的辅助线,设![]() ,
,![]() ,得到
,得到![]() ,证得△AHD∽△BHC,△DBG∽△CEG,△DFA∽△CFE,分别求得BC、EF、EG、DF、FA的长,即可求解.
,证得△AHD∽△BHC,△DBG∽△CEG,△DFA∽△CFE,分别求得BC、EF、EG、DF、FA的长,即可求解.
(1)∵∠ACB=60°,
∴优弧![]() =120°,
=120°,
∴![]() ,
,
∵D,E分别是![]() ,
,![]() 的中点,
的中点,
∴![]() ,
,
∴∠ACD+∠EDC=60°=∠CFG,
∵∠ACB=60°,
∴△CFG是等边三角形;
(2)①连结OD,
∵AC是圆O的直径,AB=12,
∴∠B=90°,
∵∠ACB=60°,
![]() ,
,
∴AC=![]() ,
,
∴OD=![]() ,
,
由(1)得:△CFG为等边三角形,
∴∠CFG=60![]() ,
,
∵点D是![]() 的中点,
的中点,
∴∠DOC=90°,
∵∠DFO=∠CFG=60°,
![]() ,
,
∴DF=8;
②由(1)得:![]() ,
,
∵D、E分别是![]() 、
、![]() 的中点,
的中点,
∴![]() =120°=
=120°=![]() ,
,
∴DE=AB=12,
ⅰ)当DF:FG=2:1时,
设FG=![]() ,DF=2
,DF=2![]() ,
,
由(1)得:△CFG为等边三角形,
∴![]() ,GE=12-3
,GE=12-3![]() ,∠CFE=60
,∠CFE=60![]() ,
,
∵![]() ,
,![]() ,
,
∴∠DCA=∠CED,∠CDE=∠ECB,
∴△DCF△CEG,
∴![]() ,
,
∴![]() ,
,
∴![]()
![]() ,
,
∴DF=![]() ,EF=12- DF=
,EF=12- DF=![]() ,
,
连结OD交AC于点M,
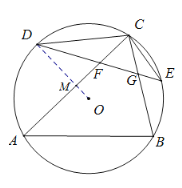
∵D是![]() 的中点,
的中点,
∴OD⊥AC,
在Rt△DMF中,∠DFM=∠CFG=60°,
∴FM=![]() DF=
DF=![]() ,
,
∴AC=2(FM+CF)= 2(![]() +
+![]() )=
)= ![]() ;
;
ⅱ)当DF:FG=1:2时,
设DF=![]() ,FG=CF=CG=2
,FG=CF=CG=2![]() ,GE=12-3
,GE=12-3![]() ,
,
同理,∴△DCF△CEG,
∴![]() ,
,
∴![]() ,
,
∴![]() =
=![]() ,
,
即DF=![]() ,EF=12- DF=
,EF=12- DF=![]() ,CF=
,CF=![]() ,
,
同理得AC=![]() ;
;
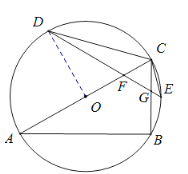
(3)作CP∥FD交BD延长线于点P,连接AD,
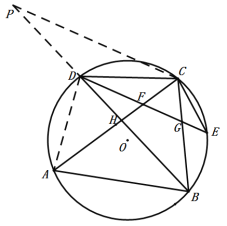
∵点D、E分别是![]() 、
、![]() 的中点,
的中点,
∴∠CDF=∠FDH,AD=DC,
∵CP∥FD,
∴∠FDC=∠DCP,∠CPD=∠FDH,![]() ,
,
∴∠DCP=∠CPD,
∴PD=CD,
∴![]() ,
,
∵![]() ,
,
∴设![]() ,
,![]() ,则
,则![]() ,
,
∴![]() ,
,
∵![]() ,∠AHD=∠BHC,
,∠AHD=∠BHC,
∴∠DAH=∠CBH,
∴△AHD∽△BHC,
∴![]() ,即
,即![]() ,
,
∴ ,
,
∴![]() ;
;
由(1)得:△CFG为等边三角形,
∴![]() ,∠CFE=60
,∠CFE=60![]() ,
,
∵![]() ,
,
∴∠HBC=∠CEF,
∴△HBC∽△CEF,
∴![]() ,即
,即 ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵∠DBG=∠CEG,∠DGB=∠CGE,
∴△DBG∽△CEG,
∴![]() ,即
,即 ,
,
∴![]() ;
;
∴![]() ,
,
同理:∴△DFA∽△CFE,
∴![]() ,即
,即 ,
,
∴![]() ;
;
∴![]() ,
,
∴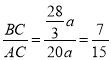 .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 过A(-1,0)、B(3,0),直线AD交抛物线于点D,点D的横坐标为2,点P(m,n)是线段AD上的动点.
过A(-1,0)、B(3,0),直线AD交抛物线于点D,点D的横坐标为2,点P(m,n)是线段AD上的动点.
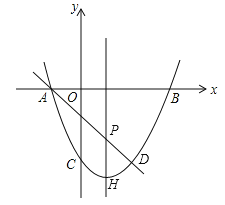
(1)求抛物线和直线AD的解析式;
(2)过点P的直线垂直于x轴,交抛物线于点H,
①求线段PH的长度l与m的关系式;
②当PH=2时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)与x轴交于点A、B,与y轴分别交于点C,其中点A(﹣1,0),OB=4OA,OC=2OA
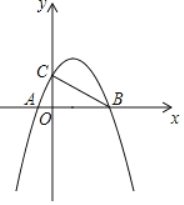
(1)求抛物线的解析式.
(2)点P是线段AB一动点,过P作PD∥AC交BC于D,当△PCD面积最大时,求点P的坐标.
(3)点M是位于线段BC上方的抛物线上一点,当∠ABC恰好等于△BCM中的某个角时,直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
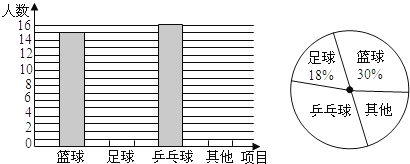
【题目】在大课间活动中,同学们积极参加体育锻炼,小明就本班同学“我最喜爱的体育项目”进行了一次调查统计,下面是他通过收集数据后,绘制的两幅不完整的统计图.请你根据图中提供的信息,解答以下问题:
(1)该班共有 名学生;
(2)补全条形统计图;
(3)在扇形统计图中,“乒乓球”部分所对应的圆心角度数为 ;
(4)学校将举办体育节,该班将推选5位同学参加乒乓球活动,有3位男同学(A,B,C)和2位女同学(D,E),现准备从中选取两名同学组成双打组合,用树状图或列表法求恰好选出一男一女组成混合双打组合的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年突如其来的肺炎疫情,给我们的生活和学习带来了诸多不便.图1是2月1日至2月5日全国“新冠肺炎”疫情新增数据统计图,为了控制疫情蔓延扩散,国家全面落实疫情防控工作,举国上下众志成城,图2是3月5日至3月9日全国“新冠肺炎”疫情新增数据统计图,请根据统计图解答以下问题:
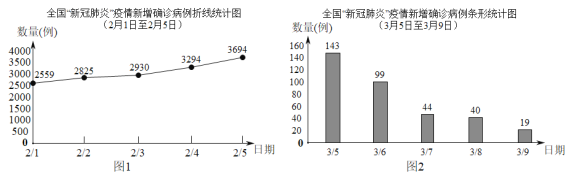
(1)写出2月3日全国新增确诊病例数,并计算3月5日至3月9日全国新增确诊病例数的平均数.
(2)对比两幅统计图中的数据,选择一个角度分析评价此次疫情控制情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
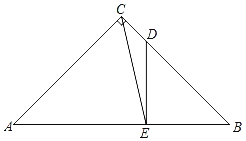
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC=4,点D在边BC上,且BD=3CD,DE⊥AB,垂足为点E,联结CE.
(1)求线段AE的长;
(2)求∠ACE的余切值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小微企业为加快产业转型升级步伐,引进一批A,B两种型号的机器.已知一台A型机器比一台B型机器每小时多加工2个零件,且一台A型机器加工80个零件与一台B型机器加工60个零件所用时间相等.
(1)每台A,B两种型号的机器每小时分别加工多少个零件?
(2)如果该企业计划安排A,B两种型号的机器共10台一起加工一批该零件,为了如期完成任务,要求两种机器每小时加工的零件不少于72件,同时为了保障机器的正常运转,两种机器每小时加工的零件不能超过76件,那么A,B两种型号的机器可以各安排多少台?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com