
【题目】下框中是小明对一道题目的解答以及老师的批改.
题目:某村计划建造如图所示的矩形蔬菜温室,要求长与宽的比为2∶1,在温室内,沿前侧内墙保留3 m的空地,其他三侧内墙各保留1 m的通道,当温室的长与宽各为多少时,矩形蔬菜种植区域的面积是288 m2?

解:设矩形蔬菜种植区域的宽为x_m,则长为2xm,
根据题意,得x·2x=288.
解这个方程,得x1=-12(不合题意,舍去),x2=12,
所以温室的长为2×12+3+1=28(m),宽为12+1+1=14(m)
答:当温室的长为28 m,宽为14 m时,矩形蔬菜种植区域的面积是288 m2.
我的结果也正确!
小明发现他解答的结果是正确的,但是老师却在他的解答中画了一条横线,并打了一个?.
结果为何正确呢?
(1)请指出小明解答中存在的问题,并补充缺少的过程:变化一下会怎样?
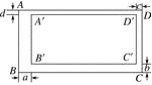
(2)如图,矩形A′B′C′D′在矩形ABCD的内部,AB∥A′B′,AD∥A′D′,且AD∶AB=2∶1,设AB与A′B′、BC与B′C′、CD与C′D′、DA与D′A′之间的距离分别为a、b、c、d,要使矩形A′B′C′D′∽矩形ABCD,a、b、c、d应满足什么条件?请说明理由.
【答案】(1)小明没有说明矩形蔬菜种植区域的长与宽之比为2∶1的理由;(2)![]() =2.
=2.
【解析】
(1)根据题意可得小明没有说明矩形蔬菜种植区域的长与宽之比为2:1的理由,所以由已知条件求出矩形蔬菜种植区域的长与宽的关系即可;
(2)由使矩形A′B′C′D′∽矩形ABCD,利用相似多边形的性质,可得![]() =
=![]() ,然后利用比例的性质.
,然后利用比例的性质.
解 (1)小明没有说明矩形蔬菜种植区域的长与宽之比为2∶1的理由.
在“设矩形蔬菜种植区域的宽为xm,则长为2xm.”前补充以下过程:
设温室的宽为xm,则长为2xm.
则矩形蔬菜种植区域的宽为(x-1-1)m,长为(2x-3-1)m.
∵![]() =
=![]() =2,
=2,
∴矩形蔬菜种植区域的长与宽之比为2∶1;
(2)要使矩形A′B′C′D′∽矩形ABCD,
就要![]() =
=![]() ,即
,即![]() =
=![]() ,
,
即![]() =
=![]() ,
,
即2AB-2(b+d)=2AB-(a+c),
∴a+c=2(b+d),
![]() =2.
=2.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案科目:初中数学 来源: 题型:
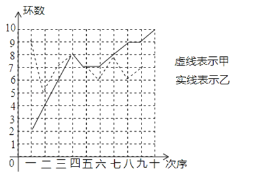
【题目】甲、乙两人在相同条件下各射靶10次,每次射靶的成绩情况如图所示:
(1)请填写下表:
平均数 | 方差 | 中位数 | 命中9环以上(包括9环)次数 | |
甲 | 7 |
|
|
|
乙 |
| 5.4 |
|
|
(2)请你就下列两个不同的角度对这次测试结果进行
①从平均数和方差相结合看(分析谁的成绩更稳定);
②从平均数和命中9环(包括9环)以上次数相结合看(分析谁的潜能更大).
查看答案和解析>>
科目:初中数学 来源: 题型:
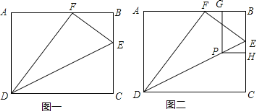
【题目】如图一,矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 上一点,将
上一点,将![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 上一点
上一点![]() 处,连结
处,连结![]() 、
、![]() .
.
![]() 求
求![]() 的长度;
的长度;
![]() 设点
设点![]() 、
、![]() 、
、![]() 分别在线段
分别在线段![]() 、
、![]() 、
、![]() 上,当
上,当![]() 且四边形
且四边形![]() 为矩形时,请说明矩形
为矩形时,请说明矩形![]() 的长宽比为
的长宽比为![]() ,并求
,并求![]() 的长.(如图二)
的长.(如图二)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场试销一种成本为每件![]() 元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于
元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于![]() ,经试销发现,销售量
,经试销发现,销售量![]() (件)与销售单价
(件)与销售单价![]() (元)符合一次函数
(元)符合一次函数![]() ,且
,且![]() 时,
时,![]() ;
;![]() 时,
时,![]() .
.
![]() 求一次函数
求一次函数![]() 的表达式;
的表达式;
![]() 若该商场获得利润为
若该商场获得利润为![]() 元,试写出利润
元,试写出利润![]() 与销售单价
与销售单价![]() 之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
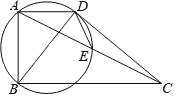
【题目】如图,四边形ABCD中,AD∥BC,∠ABC=90°,AB=5,BC=10,连接AC、BD,以BD为直径的圆交AC于点E.若DE=3,则AD的长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC,DE∥BC,那么在下列三角形中,与△EBD相似的三角形是( )

A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC∽△ADE,∠BAC =∠ADE =90°,AB=4,AC=3,F是DE的中点,若点E是直线BC上的动点,连接BF,则BF的最小值是_______.
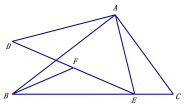
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一次函数![]() 的图象与 y轴交于点B(0,2),与反比例函数
的图象与 y轴交于点B(0,2),与反比例函数![]() 的图象交于点A (4,-1).
的图象交于点A (4,-1).
(1)求反比例函数的表达式和一次函数表达式;
(2)若点C是y轴上一点,且BC=BA,请直接写出点C的坐标.
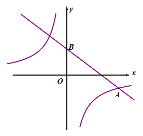
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com