
【题目】若一个三位数满足条件:其十位数字是百位数字的两倍与个位数字的差,则称这样的三位数为“十全数”,将“十全数”s的百位数字与十位数字交换位置,交换后所得的新数叫做s的“十美数”,如231是一个“十全数”,321是231的“十美数”
(1)证明:任意一个“十全数”s的“十美数”都能被3整除;
(2)已知m为“十全数”,n是m的“十美数”,若m的两倍与n的差能被13整除,求m的值
【答案】(1)见解析;(2)m为582或675或768.
【解析】
(1)首先应根据题目中所给的“十全数”和“十美数”的概念,将他们数表示出来.要说明“十美数”都能被3整除,则只需要证明到“十美数”是3的倍数即可.
(2)首先应根据题意表示出m、n,又因为m的两倍与n的差能被13整除,所以m的两倍与n的差必须是13的倍数.因此根据它们的范围一一验证即可求出最终m的值.
(1)设“十全数”s为100a+10×(2a﹣b)+b,∴s的“十美数”为100×(2a﹣b)+10a+b=210a﹣99b=3×(70a﹣33b),∴任意一个“十全数”s的“十美数”都能被3整除;
(2)设m为100x+10×(2x﹣y)+y,∴m的“十美数”为100×(2x﹣y)+10x+y=210x﹣99y,∴2[100x+10×(2x﹣y)+y]﹣[210x﹣99y]=30x+81y
∵m的两倍与n的差能被13整除,∴![]() 2x+6y
2x+6y![]() .
.
∵![]() 为整数,1≤x≤9,0≤y≤9,1≤2x﹣y≤9,∴x=1时,y=3,2x﹣y=﹣1(不合题意舍去),x=2时,y=6,2x﹣y=﹣2(不合题意舍去),x=3,4时,y的值不合题意,x=5时,y=2,2x﹣y=8,x=6时,y=5,2x﹣y=7,x=7时,y=8,2x﹣y=6,x=8、9时,y不合题意,∴m为582或675或768.
为整数,1≤x≤9,0≤y≤9,1≤2x﹣y≤9,∴x=1时,y=3,2x﹣y=﹣1(不合题意舍去),x=2时,y=6,2x﹣y=﹣2(不合题意舍去),x=3,4时,y的值不合题意,x=5时,y=2,2x﹣y=8,x=6时,y=5,2x﹣y=7,x=7时,y=8,2x﹣y=6,x=8、9时,y不合题意,∴m为582或675或768.


科目:初中数学 来源: 题型:
【题目】若等腰三角形的顶角为36°,则这个三角形就是黄金三角形。如图,在△ABC中,BA=BC,D 在边 CB 上,且 DB=DA=AC。

(1)如图1,写出图中所有的黄金三角形,并证明;
(2)若 M为线段 BC上的点,过 M作直线MH⊥AD于 H,分别交直线 AB,AC与点N,E,如图 2,试写出线段 BN、CE、CD之间的数量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全面两孩政策实施后,甲,乙两个家庭有了各自的规划.假定生男生女的概率相同,回答下列问题:
(1)甲家庭已有一个男孩,准备再生一个孩子,则第二个孩子是女孩的概率是 ;
(2)乙家庭没有孩子,准备生两个孩子,求至少有一个孩子是女孩的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
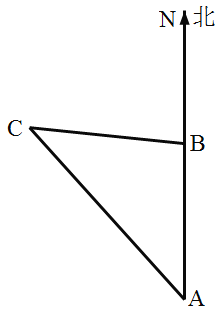
【题目】如图,上午8时,一条船从A处出发,以15海里/时的速度向正北航行,10时到达B处,从A、B望灯塔C,测得∠NAC=42°,∠NBC=84°,则从B处到灯塔C的距离_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
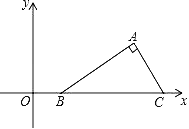
【题目】如图,在平面直角坐标系中Rt△ABC的斜边BC在x轴上,点B坐标为(1,0),AC=2,∠ABC=30°,把Rt△ABC先绕B点顺时针旋转180°,然后再向下平移2个单位,则A点的对应点A′的坐标为( )
A. (﹣4,﹣2﹣![]() ) B. (﹣4,﹣2+
) B. (﹣4,﹣2+![]() ) C. (﹣2,﹣2+
) C. (﹣2,﹣2+![]() ) D. (﹣2,﹣2﹣
) D. (﹣2,﹣2﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,D是弧BC的中点,DE⊥AC交AC的延长线于E,⊙O的切线BF交AD的延长线于F.
(1)求证:DE是⊙O的切线;
(2)若DE=4,⊙O的半径为5.求BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() ,把抛物线在
,把抛物线在![]() 轴及其上方的部分记作
轴及其上方的部分记作![]() ,将
,将![]() 向右平移得
向右平移得![]() ,
,![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() ,若直线
,若直线![]() 与
与![]() ,
,![]() 共有
共有![]() 个不同的交点,则
个不同的交点,则![]() 的取值范围是________.
的取值范围是________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com