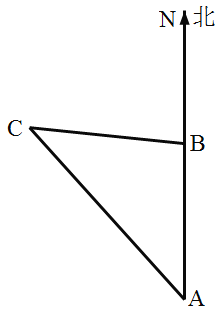
【题目】如图，上午8时，一条船从A处出发，以15海里／时的速度向正北航行，10时到达B处，从A、B望灯塔C，测得∠NAC＝42°，∠NBC=84°，则从B处到灯塔C的距离_______．
世纪百通期末金卷系列答案科目：初中数学 来源： 题型：
【题目】菱形
的边长为
，
，
、
分别是
、
的中点，
、
分别在
、
上，且
．
求证：四边形
是平行四边形；
当四边形是菱形时，求
的长；
当四边形是矩形时，求此时点到点
的距离．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列图形是由大小、形状相同的“小等边三角形”按照一定的规律组成，其中第1幅图中有3个小等边三角形，第2幅图中有8个小边三角形，第3幅图中有15个小等边三角形，依此类推，则第10幅图中有（ ）个小等边三角形．
A.63B.80C.99D.120
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】若一个三位数满足条件：其十位数字是百位数字的两倍与个位数字的差，则称这样的三位数为“十全数”，将“十全数”s的百位数字与十位数字交换位置，交换后所得的新数叫做s的“十美数”，如231是一个“十全数”，321是231的“十美数”
（1）证明：任意一个“十全数”s的“十美数”都能被3整除；
（2）已知m为“十全数”，n是m的“十美数”，若m的两倍与n的差能被13整除，求m的值
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，抛物线
与
轴交于点
，与
轴交于
，
两点（点在轴正半轴上），
为等腰直角三角形，且面积为
，现将抛物线沿
方向平移，平移后的抛物线过点时，与轴的另一点为
，其顶点为
，对称轴与轴的交点为
．
求
、
的值．
连接
，试判断
是否为等腰三角形，并说明理由．
现将一足够大的三角板的直角顶点
放在射线
或射线
上，一直角边始终过点，另一直角边与轴相交于点
，是否存在这样的点，使以点、、为顶点的三角形与
全等？若存在，求出点的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】
（1）如图1，在正方形ABCD中，M是BC边（不含端点B、C）上任意一点，P是BC延长线上一点，N是∠DCP的平分线上一点．若∠AMN=90°，求证：AM=MN．
下面给出一种证明的思路，你可以按这一思路证明，也可以选择另外的方法证明．
证明：在边AB上截取AE=MC，连ME．正方形ABCD中，∠B=∠BCD=90°，AB=BC．
∴∠NMC=180°—∠AMN—∠AMB=180°—∠B—∠AMB=∠MAB=∠MAE．
（下面请你完成余下的证明过程）
（2）若将（1）中的“正方形ABCD”改为“正三角形ABC”（如图2），N是∠ACP的平分线上一点，则当∠AMN=60°时，结论AM=MN是否还成立？请说明理由．
（3）若将（1）中的“正方形ABCD”改为“正
边形ABCD……X”，请你作出猜想：当∠AMN= °时，结论AM=MN仍然成立．（直接写出答案，不需要证明）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：在
中，
，
，
，动点
从点
出发，以每秒
个单位的速度沿
方向向终点
运动；同时，动点
也从点出发，以每秒
个单位的速度沿
方向向终点
运动．设两点运动的时间为
秒
．
连接
，在点、运动过程中，
与是否始终相似？请说明理由；
连接
，设
的面积为
，求关于的函数关系式；
连接、
，是否存在的值，使
？若存在，求出的值；若不存在，请说明理由；
探索：把
沿直线折叠成
，设
与交于点
，当
是直角三角形时，请直接写出的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
