
【题目】如图,![]() 是直角三角形,
是直角三角形,![]() ,
,![]() ,以点
,以点![]() 为旋转中心,将
为旋转中心,将![]() 旋转到
旋转到![]() 的位置,且使
的位置,且使![]() 经过点
经过点![]() .
.

![]() 求
求![]() 的度数,判断
的度数,判断![]() 的形状;
的形状;
![]() 求线段
求线段![]() 与线段
与线段![]() 的数量关系.
的数量关系.
【答案】![]() ∠ACA′=60°,
∠ACA′=60°,![]() 是等边三角形;
是等边三角形;![]() .
.
【解析】
(1)证明∠BAC=60°;证明AC=A′C,得到∠A′=∠A′AC=60°,求出∠ACA′=60°;
(2)由△ABC≌△A′B′C′得到∠A′CB=∠ACB=90°,求得∠B′=∠B=30°,由(1)知:∠ACA′=60°,得到AC=AB′,于是得到结论.
(1)∵∠ACB=90°,∠B=30°,∴AB=2AC,∠BAC=60°;
∵△ABC≌△A′B′C′,∴∠A′=∠BAC=60°,AC=A′C,∴∠A′=∠A′AC=60°,∴∠ACA′=180°﹣120°=60°,∴△ACA′是等边三角形;
(2)∵△ABC≌△A′B′C′,∴∠A′CB=∠ACB=90°,∠B′=∠B=30°,A′B′=AB,由(1)知:∠ACA′=60°,∴∠ACB′=30°,∴AC=AB′,∴AB=A′B′=AA′+AB′=2AC=2AC.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】定义:如图①,抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点,点P在该抛物线上(P点与A、B两点不重合).如果△ABP的三边满足AP2+BP2=AB2,则称点P为抛物线y=ax2+bx+c(a≠0)的勾股点.
(1)直接写出抛物线y=-x2+1的勾股点的坐标.
(2)如图②,已知抛物线y=ax2+bx(a≠0)与x轴交于A,B两点,点P(1, ![]() )是抛物线的勾股点,求抛物线的函数表达式.
)是抛物线的勾股点,求抛物线的函数表达式.
(3)在(2)的条件下,点Q在抛物线上,求满足条件S△ABQ=S△ABP的Q点(异于点P)的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在正方形ABCD中,对角线AC与BD相交于点O,OE∥AB交BC于点E.若AD=8cm,则OE的长为( )

A. 3cm B. 4cm C. 6cm D. 8cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(a,0),B(0,a),等腰直角三角形ODC的斜边经过点B,OE⊥AC,交AC于E,若OE=2,则△BOD与△AOE的面积之差为( )

A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全面两孩政策实施后,甲,乙两个家庭有了各自的规划.假定生男生女的概率相同,回答下列问题:
(1)甲家庭已有一个男孩,准备再生一个孩子,则第二个孩子是女孩的概率是 ;
(2)乙家庭没有孩子,准备生两个孩子,求至少有一个孩子是女孩的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“缤纷节”已经成为西南大学附中一张响亮的名片,受到了社会各界的高度赞扬缤纷意寓缤纷的青春,缤纷的风采,缤纷的个性,缤纷的创意,它充分展现了我校学子的青春与活力.初2020级“知义班”班委计划给全班学生购置演出服装以用于“缤纷节”晚会的舞台剧表演经与经销商沟通,男生的服装购置总价为1500元,女生的服装总价为2000元,由于女生的服装工艺较复杂,所以商家最后报出的服装单价女生比男生贵20元,其中“知义班”男女生人数相等.
(1)请问男女生的表演服装单价分别为多少元?
(2)在看到服装样品后,初2020级决定再买120套相同的服装,与商家沟通后女生服装的单价比之前降低了20%,男生服装的单价比之前降低了10%,如果年级购买这120套服装的费用不超过7300元,那么年级最多可购买多少套女生的服装?
查看答案和解析>>
科目:初中数学 来源: 题型:
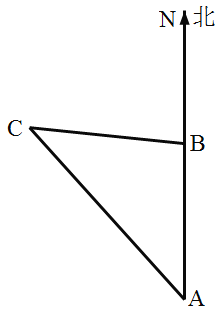
【题目】如图,上午8时,一条船从A处出发,以15海里/时的速度向正北航行,10时到达B处,从A、B望灯塔C,测得∠NAC=42°,∠NBC=84°,则从B处到灯塔C的距离_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1).
(1)在图中作出![]() 关于
关于![]() 轴对称的
轴对称的![]() .
.
(2)写出点![]() 的坐标(直接写答案).
的坐标(直接写答案).
A1_____________,B1______________,C1______________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. “明天降雨的概率是![]() ”表示明天有
”表示明天有![]() 的时间降雨
的时间降雨
B. “彩票中奖的概率是![]() ”表示买
”表示买![]() 张彩票一定会中奖
张彩票一定会中奖
C. “抛一枚硬币正面朝上的概率是![]() ”表示每抛
”表示每抛![]() 次就有
次就有![]() 次出现正面朝上
次出现正面朝上
D. “抛一枚普通的正方体骰子,出现朝正面的数为奇数的概率是![]() ”表示如果这个骰子抛很多很多次,那么平均每
”表示如果这个骰子抛很多很多次,那么平均每![]() 次就有
次就有![]() 次出现朝正面的数为奇数
次出现朝正面的数为奇数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com