【题目】如图，抛物线
与
轴交于点
，
，把抛物线在轴及其上方的部分记作
，将向右平移得
，与轴交于点，
，若直线
与，共有
个不同的交点，则
的取值范围是________．
【答案】
【解析】
首先求出点A和点B的坐标，然后求出C2解析式，分别求出直线y＝x＋m与抛物线C2相切时m的值以及直线y＝x＋m过点B时m的值，结合图形即可得到答案.
令y＝－2x2＋8x－6＝0，即x2－4x＋3＝0，解得x＝1或x＝3，则点A（1,0），B(3,0)由于C1向右平移两个长度单位得C2,则C2解析式为y＝－2（x－4）2＋2（3≤x≤5），当y＝x＋m1与C2相切时，令y＝x＋m1＝y＝－2（x－4）2＋2，即2x2－15x＋30＋m1＝0，△＝－8m1－15＝0，解得m1＝－
，当y＝x＋m2过点B时，即0＝3＋m2，m2＝－3，当－3＜m＜－时直线y＝x＋m与C1、C2共有3个不同交点，故答案是－3＜m＜－.
导学教程高中新课标系列答案
小学课时特训系列答案科目：初中数学 来源： 题型：
【题目】若一个三位数满足条件：其十位数字是百位数字的两倍与个位数字的差，则称这样的三位数为“十全数”，将“十全数”s的百位数字与十位数字交换位置，交换后所得的新数叫做s的“十美数”，如231是一个“十全数”，321是231的“十美数”
（1）证明：任意一个“十全数”s的“十美数”都能被3整除；
（2）已知m为“十全数”，n是m的“十美数”，若m的两倍与n的差能被13整除，求m的值
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB=AC，AD和CE是高，∠ACE=45°，点F是AC的中点，AD与FE，CE分别交于点G、H，∠BCE=∠CAD，有下列结论：①图中存在两个等腰直角三角形；②△AHE≌△CBE；③BCAD=
AE2；④S△ABC=4S△ADF．其中正确的个数有（ ）
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知∠1=∠2，则下列条件中不一定能使△ABC≌△ABD的是( )
A. AC=AD B. BC=BD C. ∠C=∠D D. ∠3=∠4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一个不透明的布袋里装有16个只有颜色不同的球，其中红球有x个，白球有2x个，其他均为黄球，现甲从布袋中随机摸出一个球，若是红球则甲同学获胜，甲同学把摸出的球放回并搅匀，由乙同学随机摸出一个球，若为黄球，则乙同学获胜。
（1）当X=3时，谁获胜的可能性大？
（2）当x为何值时，游戏对双方是公平的？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：在
中，
，
，
，动点
从点
出发，以每秒
个单位的速度沿
方向向终点
运动；同时，动点
也从点出发，以每秒
个单位的速度沿
方向向终点
运动．设两点运动的时间为
秒
．
连接
，在点、运动过程中，
与是否始终相似？请说明理由；
连接
，设
的面积为
，求关于的函数关系式；
连接、
，是否存在的值，使
？若存在，求出的值；若不存在，请说明理由；
探索：把
沿直线折叠成
，设
与交于点
，当
是直角三角形时，请直接写出的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
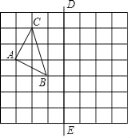
【题目】如图，在所给的网格图中，完成下列各题（用直尺画图，否则不给分）
（1）画出格点△ABC关于直线DE的对称的△A1B1C1；
（2）在DE上画出点P，使PA+PC最小；
（3）在DE上画出点Q，使QA﹣QB最大．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，对于点P（a，b）和点Q（a，b'），给出如下定义：
若b'=
，则称点Q为点P的限变点．例如：点（3，﹣2）的限变点的坐标是（3，﹣2），点（﹣1，5）的限变点的坐标是（﹣1，﹣5）．
（1）①点（﹣
，1）的限变点的坐标是 ；
②在点A（﹣1，2），B（﹣2，﹣1）中有一个点是函数y=
图象上某一个点的限交点，这个点是 ；
（2）若点P在函数y=﹣x+3的图象上，当﹣2≤x≤6时，求其限变点Q的纵坐标b'的取值范围；
（3）若点P在关于x的二次函数y=x2﹣2tx+t2+t的图象上，其限变点Q的纵坐标b'的取值范围是b'≥m或b'＜n，其中m＞n．令s=m﹣n，求s关于t的函数解析式及s的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
