Question

【题目】如图，在中， ， ，点在边上，且，以为圆心， 长为半径的圆分别交, 于, 两点.

（1）求证： 是的切线；

（2）判断由, , 及切点所构成的四边形的形状，并说明理由.

Answer 1

【答案】（1）证明见解析；（2）四边形为菱形，理由见解析.

【解析】试题分析：（1）作OF⊥AC于F，如图，理由三角函数可得到∠A=30°，OA=2OF，再利用BO=AB得到OA=2OB，所以OF=OB，于是根据切线的判定方法可判AC是⊙O的切线；（2）先证明△OFD和△OBE都是等边三角形得到OD=DF，∠BOE=60°，则可计算出∠EOF=60°，从而可判定△OEF为等边三角形，所以EF=OE，则有OD=DF=EF=OE，然后根据菱形的判定方法可判断四边ODFE为菱形．

试题解析：

(1)证明：作OF⊥AC于F，如图，

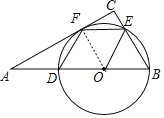
∵∠C=90°，AB=2BC，

∴sinA==，

∴∠A=30°，

∴OA=2OF，

∵BO=AB，

∴OA=2OB，

∴OF=OB，

∴AC是⊙O的切线；

(2)四边形ODFE为菱形。理由如下：

∵∠A=30°，

∴∠AOF=∠B=60°，

∴△OFD和△OBE都是等边三角形，

∴OD=DF,∠BOE=60°，

∴∠EOF=180°60°60°=60°，

∴△OEF为等边三角形，

∴EF=OE，

∴OD=DF=EF=OE，

∴四边形ODFE为菱形。