Question

【题目】如图，∠AOB=90°，OM平分∠AOB，将直角三角板的顶点P在射线OM上移动，两直角边分别与OA、OB相交于点C、D，问PC与PD相等吗？试说明理由．

Answer 1

【答案】解：PC与PD相等．理由如下：过点P作PE⊥OA于点E，PF⊥OB于点F．
∵OM平分∠AOB，点P在OM上，PE⊥OA，PF⊥OB，
∴PE=PF（角平分线上的点到角两边的距离相等）
又∵∠AOB=90°，∠PEO=∠PFO=90°，
∴四边形OEPF为矩形，
∴∠EPF=90°，
∴∠EPC+∠CPF=90°，
又∵∠CPD=90°，
∴∠CPF+∠FPD=90°，
∴∠EPC=∠FPD=90°﹣∠CPF．
在△PCE与△PDF中，
∵ ，
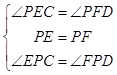∴△PCE≌△PDF（ASA），
∴PC=PD．

【解析】先过点P作PE⊥OA于点E，PF⊥OB于点F，构造全等三角形：Rt△PCE和Rt△PDF，这两个三角形已具备两个条件：90°的角以及PE=PF，只需再证∠EPC=∠FPD，根据已知，两个角都等于90°减去∠CPF，那么三角形全等就可证．
【考点精析】利用角平分线的性质定理对题目进行判断即可得到答案，需要熟知定理1：在角的平分线上的点到这个角的两边的距离相等； 定理2：一个角的两边的距离相等的点，在这个角的平分线上．