
【题目】如图,在正方形![]() 中,过
中,过![]() 作一直线与
作一直线与![]() 相交于点
相交于点![]() ,过
,过![]() 作
作![]() 垂直
垂直![]() 于点
于点![]() ,过
,过![]() 作
作![]() 垂直
垂直![]() 于点
于点![]() ,在
,在![]() 上截取
上截取![]() ,再过
,再过![]() 作
作![]() 垂直
垂直![]() 交
交![]() 于
于![]() .若
.若![]() .则
.则![]() 与四边形
与四边形![]() 的面积之和为________.
的面积之和为________.

【答案】9
【解析】
由ABCD为正方形,根据正方形的性质得到AB=BC,∠ABC=90°,即∠CBG+∠ABF=90°,又根据CG与BE垂直得到∠BCG+∠CBG=90°,根据同角的余角相等得到一对角相等,又根据一对直角相等,利用“AAS”即可得到三角形BCG与三角形FBA全等,根据全等三角形的对应边相等得到AF与BG相等,又因为FH=FB,从而得到AH=FG,然后由垂直得到一对直角相等,加上一个公共角,得到三角形APH与三角形ABF相似,根据相似得比例,设AH=FG=x,用x表示出PH,由四边形PHFB一组对边平行,另一组对边不平行得到此四边形为梯形,根据梯形的面积公式,由上底PH,下底为BF=3,高FH=3,表示出梯形的面积;然后在三角形BCG与三角形ECG中,根据同角的余角相等,再加上一对直角得到两三角形相似,根据相似得比例,用含x的式子表示出GE,由CG=3,表示出的GE,利用三角形的面积公式表示出直角三角形CGE的面积,把表示出的两面积相加,化简即可得到结论.
∵四边形ABCD为正方形,∴AB=BC,∠ABC=90°,即∠CBG+∠ABF=90°,又CG⊥BE,即∠BGC=90°,∴∠BCG+∠CBG=90°,∴∠ABF=∠BCG,又AF⊥BG,∴∠AFB=∠BGC=90°,∴△ABF≌△BCG,∴AF=BG,BF=CG=FH=3.
又∵FH=BF,∴AH=FG,设AH=FG=x.
∵PH⊥AF,BF⊥AF,∴∠AHP=∠AFB=90°,又∠PAH为公共角,∴△APH∽△ABF,∴![]() =
=![]() ,即PH=
,即PH=![]() .
.
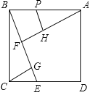
∵PH∥BF,BP不平行FH,∴四边形BFHP为梯形,其面积为![]() =
=![]() +
+![]() ;
;
又∵∠BCG+∠ECG=90°,∠ECG+∠BEC=90°,∴∠BCG=∠BEC,又∠BGC=∠CGE=90°,∴△BCG∽△CEG,∴![]() =
=![]() ,即GE=
,即GE=![]() ,故Rt△CGE的面积为
,故Rt△CGE的面积为![]() ×3×
×3×![]() ,则△CGE与四边形BFHP的面积之和为
,则△CGE与四边形BFHP的面积之和为![]() +
+![]() +
+![]() =
=![]() +
+![]() =9.
=9.
故答案为:9.


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB.添加一个条件,不能使四边形DBCE成为矩形的是( )

(A)AB=BE (B)BE⊥DC (C)∠ADB=90° (D)CE⊥DE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 为
为![]() 斜边
斜边![]() 上的一点,以
上的一点,以![]() 为半径的
为半径的![]() 与边
与边![]() 交于点
交于点![]() ,与边
,与边![]() 交于点
交于点![]() ,连接
,连接![]() ,且
,且![]() 平分
平分![]() .
.

![]() 试判断
试判断![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
![]() 若
若![]() ,
,![]() ,求阴影部分的面积(结果保留
,求阴影部分的面积(结果保留![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工人师傅用![]() 米长的铝合金材料制作一个如图所示的矩形窗框,图中的①、②、③区域都是矩形,且
米长的铝合金材料制作一个如图所示的矩形窗框,图中的①、②、③区域都是矩形,且![]() ,
,![]() ,
,![]() 分别是
分别是![]() 、
、![]() 的中点.(说明:图中黑线部分均需要使用铝合金材料制作,铝合金材料宽度忽略不计).
的中点.(说明:图中黑线部分均需要使用铝合金材料制作,铝合金材料宽度忽略不计).

![]() 当矩形窗框
当矩形窗框![]() 的透光面积是
的透光面积是![]() 平方米时,求
平方米时,求![]() 的长度.
的长度.
![]() 当
当![]() 为多长时,矩形窗框
为多长时,矩形窗框![]() 的透光面积最大?最大面积是多少?
的透光面积最大?最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两个箱子,其中甲箱内有![]() 颗球,分别标记号码
颗球,分别标记号码![]() ,且号码为不重复的整数,乙箱内没有球.已知小育从甲箱内拿出
,且号码为不重复的整数,乙箱内没有球.已知小育从甲箱内拿出![]() 颗球放入乙箱后,乙箱内球的号码的中位数为
颗球放入乙箱后,乙箱内球的号码的中位数为![]() .若此时甲箱内有
.若此时甲箱内有![]() 颗球的号码小于
颗球的号码小于![]() ,有
,有![]() 颗球的号码大于
颗球的号码大于![]() ,若他们的中位数都为
,若他们的中位数都为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG⊥CE于G, CD=AE.
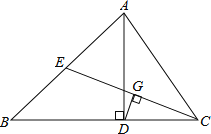
(1)求证: CG=EG.
(2)已知BC=13, CD=5,连结ED,求△EDC 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】感知:如图1,在![]() 中,D、E分别是AB、AC两边的中点,延长DE至点F,使
中,D、E分别是AB、AC两边的中点,延长DE至点F,使![]() ,连结
,连结![]() 易知
易知![]() ≌
≌![]() .
.



探究:如图2,AD是![]() 的中线,BE交AC于点E,交AD于点F,且
的中线,BE交AC于点E,交AD于点F,且![]() ,求证:
,求证:![]() .
.
应用:如图3,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,DE是
,DE是![]() 的中位线
的中位线![]() 过点D、E作
过点D、E作![]() ,分别交边BC于点F、G,过点A作
,分别交边BC于点F、G,过点A作![]() ,分别与FD、GE的延长线交于点M、N,则四边形MFGN周长C的取值范围是______.
,分别与FD、GE的延长线交于点M、N,则四边形MFGN周长C的取值范围是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com