Question

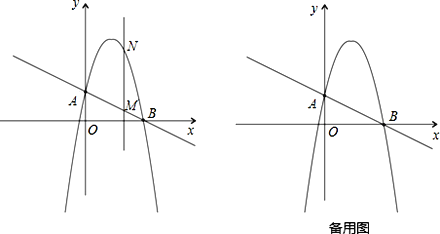
【题目】如图，一次函数分别交y轴、x 轴于A、B两点，抛物线过A、B两点.

（1）求这个抛物线的解析式；

（2）作垂直x轴的直线x=t，在第一象限交直线AB于点M，交这个抛物线于点N.求当t 取何值时，MN有最大值？最大值是多少？

（3）在（2）的情况下，以A、M、N、D为顶点作平行四边形，求第四个顶点D的坐标.

Answer 1

【答案】（1）抛物线解析式为 ；

（2）当 t=2 时，MN有最大值为 4；

（3）D（0，6）或（0，-2）或（4，4）.

【解析】试题分析：

（1）先由直线分别交y轴、x轴于点A、B这一条件求出点A、B的坐标，将所求坐标代入抛物线列出关于的值即可得到所求抛物线的解析式；

（2）如图1，由题意可知点M的横坐标为t，根据点M在直线上，点N在（1）中所求抛物线上，可用含“t”的代数式表达出点M、N的坐标，结合第一象限中，点N在点M的上方，可用含“t”的代数式表达出MN的长，把所得式子配方，即可得到所求答案；

（3）由（2）中答案可得求得对应的点A、M、N的坐标，如图2分析可知点D有三种可能，其中两种情况点D在y轴上，结合AD=MN，即可求得两个符合要求的点D1、D2的坐标；由图可知第三个符合要求点D就是直线D1N和D2M的交点，求出两直线的解析式联立成方程组，解方程组即可求得第三个符合要求的点D的坐标.

试题解析：

(1)∵分别交y轴、x轴于A.、B两点，

∴A、B点的坐标为：A(0,2)，B(4,0)，

将x=0，y=2代入y=x+bx+c得c=2，

将x=4，y=0，c=2代入y=x+bx+c得0=16+4b+2，解得b=，

∴抛物线解析式为： ，

(2)如图1，由题意可知，直线MN即是直线，

∵点M在直线上，点N在抛物线上，

∴点M、N的坐标分别为、，

∵在第一象限中，点N在点M的上方，

∴MN=，

∴当时，MN最长=4；

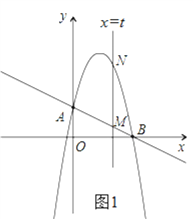
(3)由(2)可知，A(0，2)，M(2，1)，N(2，5).

以A. M、N、D为顶点作平行四边形，D点的可能位置有三种情形，如图2所示：

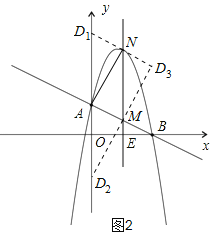
(i)当D在y轴上时，设D的坐标为(0，a)

由AD=MN，得|a2|=4，解得a1=6，a2=2，

从而D1为(0，6)或D2(0，2)，

(ii)当D不在y轴上时，由图可知D3为D1N与D2M的交点，

由D1、D2、M、N的坐标可求得直线D1N的解析式为：y=x+6，直线D2M的解析式为：y=x2，

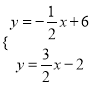由 解得 ，

∴D3的坐标为：(4，4)，

综上所述，所求的D点坐标为(0，6)，(0，2)或(4，4).