
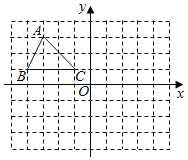
【题目】如图,已知A(﹣3,3)、B(﹣4,1)、C(﹣1,1)是平面直角坐标系上的三点.
(1)请画出△ABC绕点O逆时针旋转90°后的△A1B1C1;
(2)请画出△A1B1C1关于y轴对称△A2B2C2;
(3)判断以A、A1、A2为顶点的三角形的形状.(无需说明理由)
 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
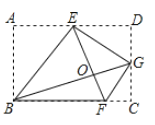
【题目】将矩形ABCD按如图所示的方式折叠,BE,EG,FG为折痕,若顶点A,C,D都落在点O处,且点B,O,G在同一条直线上,同时点E,O,F在另一条直线上,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 切
切![]() 于点
于点![]() ,点
,点![]() 是
是![]() 上的一个动点(点
上的一个动点(点![]() 不与
不与![]() ,
,![]() 两点重合),连接
两点重合),连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.
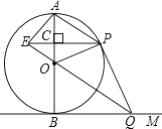
(1)求证:直线![]() 为
为![]() 的切线;
的切线;
(2)若直径![]() 的长为4.
的长为4.
①当![]() ________时,四边形
________时,四边形![]() 为正方形;
为正方形;
②当![]() ________时,四边形
________时,四边形![]() 为菱形.
为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
如图1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,连接AC,BD交于点M.填空:
①![]() 的值为 ;
的值为 ;
②∠AMB的度数为 .
(2)类比探究
如图2,在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC交BD的延长线于点M.请判断![]() 的值及∠AMB的度数,并说明理由;
的值及∠AMB的度数,并说明理由;
(3)拓展延伸
在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M,若OD=1,OB=![]() ,请直接写出当点C与点M重合时AC的长.
,请直接写出当点C与点M重合时AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
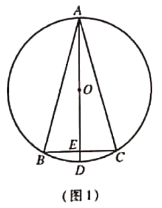
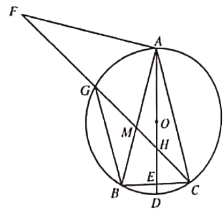
【题目】已知:![]() 是
是![]() 的内接三角形,且
的内接三角形,且![]() ,直径
,直径![]() 交
交![]() 于点
于点![]() .
.
![]() 如图1 ,求证:
如图1 ,求证:![]() ;
;
![]() 如图2,将线段
如图2,将线段![]() 绕点
绕点![]() 顺时针旋转得到线段
顺时针旋转得到线段![]() ,旋转角为
,旋转角为![]() 连接
连接![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,连接
,连接![]() ,求证:
,求证: ![]() ;
;
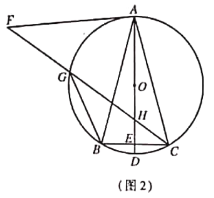
![]() 如图3,在(2)的条件下,当
如图3,在(2)的条件下,当![]() 时,
时,![]() 交
交![]() 于点
于点![]() 若
若![]() 求
求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】央视举办的《中国诗词大会》受到广大学生群体广泛关注.某校的诗歌朗诵社团就《中国诗词大会》节目的喜爱程度,在校内对部分学生进行了问卷调查,并对问卷调查的结果分为“非常喜欢”、“比较喜欢”、“感觉一般”、“不太喜欢”四个等级,分别记作A、B、C、D.根据调查结果绘制出如图所示的扇形统计图和条形统计图,请结合图中说给信息解答下列问题:
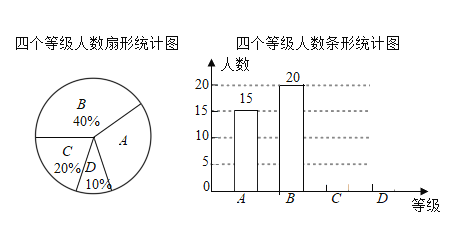
(1)本次被调查对象共有 人,扇形统计图中被调查者“非常喜欢”等级所对应圆心角的度数为 ;
(2)将条形统计图补充完整,并标明数据;
(3)若选“不太喜欢”的人中有两名女生,其余是男生,从原“不太喜欢”的人中挑选两名学生了解不太喜欢的原因,请用画树状图或列表法求所选取的这两名学生恰好是一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
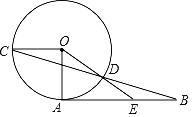
【题目】如图,AB是⊙O的切线,OA,OC是⊙O的半径,且OC∥AB,连接BC交⊙O于点D,点D恰为BC的中点,连接OD并延长,交AB于点E.
(1)求∠B的度数;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书店以![]() 元的价格购进一批科普书进行销售,物价局根据市场行情规定,销售单价不低于
元的价格购进一批科普书进行销售,物价局根据市场行情规定,销售单价不低于![]() 元且不高于
元且不高于![]() 元.在销售中发现,该科普书的每天销售数量
元.在销售中发现,该科普书的每天销售数量![]() (本)与销售单价
(本)与销售单价![]() (元)之间存在某种函数关系,对应如下:
(元)之间存在某种函数关系,对应如下:
销售单价 |
|
|
|
|
|
销售数量 |
|
|
|
|
|
(1)用你所学过的函数知识,求出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)请问该科普书每天利润![]() (元)的最大值是多少?
(元)的最大值是多少?
(3)如果该科普书每天利润必须不少于![]() 元,试求出每天销售数量
元,试求出每天销售数量![]() 最少为多少本?
最少为多少本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】滴滴快车是一种便捷的出行工具,某地的计价规则如表:
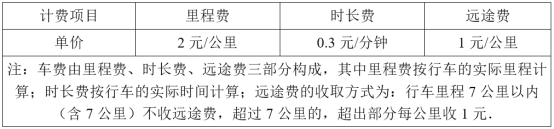
小李与小张分别从不同地点,各自同时乘坐滴滴快车,到同一地点相见,已知到达约定地点时他们的实际行车里程分别为7公里与9公里,两人付给滴滴快车的乘车费相同.其中一人先到达约定地点,他等候另一人的时间等于他自己实际乘车时间,且恰好是另一人实际乘车时间的一半,则小李的乘车费为_____元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com