
【题目】如图,矩形OABC的顶点A、C分别在![]() 的正半轴上,点B的坐标为(3,4)一次函数
的正半轴上,点B的坐标为(3,4)一次函数![]() 的图象与边OC、AB分别交于点D、E,并且满足OD= BE.点M是线段DE上的一个动点.
的图象与边OC、AB分别交于点D、E,并且满足OD= BE.点M是线段DE上的一个动点.
(1)求b的值;
(2)连结OM,若三角形ODM的面积与四边形OAEM的面积之比为1:3,求点M的坐标;
(3)设点N是![]() 轴上方平面内的一点,以O、D、M、N为顶点的四边形是菱形,求点N的坐标.
轴上方平面内的一点,以O、D、M、N为顶点的四边形是菱形,求点N的坐标.

【答案】(1)![]() ;
;
(2)M(1, ![]() );
);
(3)当四边形OMDN是菱形时,M(![]() ,
,![]() )N(
)N(![]() ,
,![]() )
)
【解析】分析:(1)首先在一次函数的解析式中令x=0,即可求得D的坐标,则OD的长度即可求得,OD=b,则E的坐标即可利用b表示出来,然后代入一次函数解析式即可得到关于b的方程,求得b的值;(2)首先求得四边形OAED的面积,则△ODM的面积即可求得,设出M的横坐标,根据三角形的面积公式即可求得M的横坐标,进而求得M的坐标;(3)分成四边形OMDN是菱形和四边形OMND是菱形两种情况进行讨论,四边形OMDN是菱形时,M是OD的中垂线与DE的交点,M关于OD的对称点就是N;四边形OMND是菱形,OM=OD,M在直角DE上,设出M的坐标,根据OM=OD即可求得M的坐标,则根据ON和DM的中点重合,即可求得N的坐标.
本题解析:(1)y=![]() x+b中,令x=0,解得y=b,则D的坐标是(0,b),OD=b,
x+b中,令x=0,解得y=b,则D的坐标是(0,b),OD=b,
∵OD=BE,
∴BE=b,则E的坐标是(3,4b),
把E的坐标代入y=![]() x+b得4b=2+b,
x+b得4b=2+b,
解得:b=3;
(2) ![]() ,
,
∵三角形ODM的面积与四边形OAEM的面积之比为1:3,
∴![]() .
.
设M的横坐标是a,则![]() ×3a=1.5,解得:a=1,
×3a=1.5,解得:a=1,
把x=a=1代入y=![]() x+3得y=
x+3得y=![]() ×
×![]() +3=
+3=![]() .
.
则M的坐标是(1, ![]() );
);
(3)当四边形OMDN是菱形时,如图(1),M的纵坐标是![]() ,把y=
,把y=![]() 代入y=
代入y=![]() x+3,得
x+3,得![]() x+3=
x+3=![]() ,解得:x=
,解得:x=![]() ,
,
则M的坐标是(![]() ,
,![]() ),
),
则N的坐标是(![]() ,
,![]() );
);
当四边形OMND是菱形时,如图(2)OM=OD=3,设M的横坐标是m,则纵坐标是![]() m+3,则
m+3,则![]() ,
,
解得:m=![]() 或0(舍去).
或0(舍去).
则M的坐标是(![]() ,
,![]() ).
).
则DM的中点是(![]() ,
,![]() ).
).
则N的坐标是(![]() ,
,![]() ).
).
故N的坐标是(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】一个正方体的六个面上分别标有﹣1,﹣2,﹣3,﹣4,﹣5,﹣6中的一个数,各个面上所标数字都不相同,如图是这个正方体的三种放置方法,三个正方体下底面所标数字分别是a,b,c,则a+b+c+abc= .

查看答案和解析>>
科目:初中数学 来源: 题型:
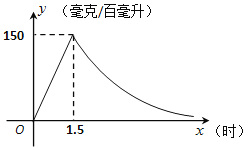
【题目】实验数据显示,一般成人喝半斤低度白酒后,1.5小时内其血液中酒精含量![]() (毫克/百毫升)与时间
(毫克/百毫升)与时间![]() (时)成正比例;1.5小时后(包括1.5小时)
(时)成正比例;1.5小时后(包括1.5小时)![]() 与
与![]() 成反比例.根据图中提供的信息,解答下列问题:
成反比例.根据图中提供的信息,解答下列问题:
(1)求一般成人喝半斤低度白酒后, ![]() 与
与![]() 之间的两个函数关系式及相应的自变量
之间的两个函数关系式及相应的自变量![]() 取值范围;
取值范围;
(2)依据人的生理数据显示,当![]() ≥80时,肝部正被严重损伤,请问喝半斤低度白酒后,肝部被严重损伤持续多少小时?
≥80时,肝部正被严重损伤,请问喝半斤低度白酒后,肝部被严重损伤持续多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
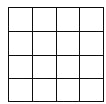
【题目】(1)如上图,正方形网格中的每个小正方形边长都是1,任意连接这些小正方形的顶点,可得到一些线段;请在图中画出AB=![]() ,CD=
,CD=![]() ,EF=
,EF=![]() 这样的线段;
这样的线段;
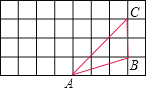
(2)如图所示,在边长为1的网格中作出△ABC绕点A按逆时针方向旋转90°后的图形△ABC;并计算对应点B和B之间的距离?
(3)如图是由5个边长为1的小正方形拼成的.
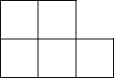
①将该图形分成三块(在图中画出),使由这三块可拼成一个正方形;
②求出所拼成的正方形的面积S.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个工程队共同承担一项筑路任务,甲队单独施工完成此项任务比乙队单独施工完成此项任务多用10天,且甲队单独施工45天和乙队单独施工30天的工作量相同.
(1)甲、乙两队单独完成此项任务各需多少天?
(2)若甲、乙两队共同工作了3天后,乙队因设备检修停止施工,由甲队继续施工,为了不影响工程进度,甲队的工作效率提高到原来的2倍,要使甲队总的工作量不少于乙队的工作量的2倍,那么甲队至少再单独施工多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
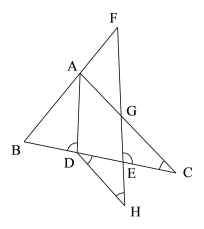
【题目】如图,在△ABC中,AD平分∠BAC交BC于点D,点F在BA的延长线上,点E在线段CD上,EF与AC相交于点G,AD∥EF.
(1)求证:∠BDA+∠CEG=180°;
(2)若点H在FE的延长线上,且∠F=∠H,则∠EDH与∠C相等吗,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李先生在2018年9月第14周星期五股市收盘时,以每股9元的价格买进某公司的股票1000股,在9月第3周的星期一至星期五,该股票每天收盘时每股的涨跌(单位:元)情况如下表:注:表中记录的数据为每天收盘价格与前一天收盘价格的变化量,星期一的数据是与上星期五收盘价格的变化量.

(1)请你判断在9月的第3周内,该股票价格收盘时,价格最高的是哪一天?
(2)在9月第3周内,求李先生购买的股票每股每天平均的收盘价格.(结果精确到百分位)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图已知P为⊙O外一点,PA为⊙O的切线,B为⊙O上一点,且PA=PB,C为优弧 ![]() 上任意一点(不与A、B重合),连接OP、AB,AB与OP相交于点D,连接AC、BC.
上任意一点(不与A、B重合),连接OP、AB,AB与OP相交于点D,连接AC、BC.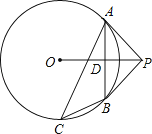
(1)求证:PB为⊙O的切线;
(2)若tan∠BCA= ![]() ,⊙O的半径为
,⊙O的半径为 ![]() ,求弦AB的长.
,求弦AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是由若干个小圆圈堆成的一个形如等边三角形的图案,最上面一层有一个圆圈,
以下各层均比上一层多一个圆圈,一共堆了n 层.将图1倒置后与原图1拼成图2的形状,这样我们可以
算出图1中所有圆圈的个数为1+2+3+…+n=![]() .
.

如果图中的圆圈共有13层,请解决下列问题:
(1)我们自上往下,在每个圆圈中按图3的方式填上一串连续的正整数1,2,3,4,……,则最底层最左
边这个圆圈中的数是 ;
(2)我们自上往下,在每个圆圈中按图4的方式填上一串连续的整数-23,-22,-21,-20,……,求
最底层最右边圆圈内的数是_______;
(3)求图4中所有圆圈中各数的绝对值之和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com