
【题目】某校组织春游活动,提供了A、B、C、D四个景区供学生选择,并把选择最多的景区作为本次春游活动的目的地。经过抽样调查,并将采集的数据绘制成如下两幅不完整的统计图,请根据图①、②所提供的信息,解答下列问题:

(1)本次抽样调查的学生有______名,其中选择景区A的学生的频率是______:
(2)请将图②补充完整:
(3)若该校共有1200名学生,根据抽样调查的结果估计全校共有多少名学生选择景区C?(要有解答过程)
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
【题目】某病人每天下午需要测量一次血压,下表是该病人本周星期一至星期五收缩压的变化情况.(“+”表示上升,“-”表示下降)
星期 | 一 | 二 | 三 | 四 | 五 |
收缩压的变化(与前一天比较) | +30 | -20 | +17 | +18 | -20 |
(1)本周三与周一相比较收缩压________了;(填“上升”或“下降”)
(2)通过计算说明本周五收缩压与上周日相比是上升了还是下降了,并求出上升或下降了多少;
(3)如果该病人本周五的收缩压为185,那么他上个周日的收缩压为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】1883年,康托尔构造的这个分形,称做康托尔集,从长度为1的线段开始,康托尔取走其中间三分之一而达到第一阶段;然后从每人个余下的三分之一线段中取走中间三分之一而达到第二阶段,无限地重复这一过程,余下的无穷点就称做康托尔集,下图是康托尔集的最初几个阶段,当达到第5个阶段时,取走的所有线段的长度之和为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明,请你利用图1或图2证明勾股定理(其中∠DAB=90°)
求证:a2+b2=c2.

查看答案和解析>>
科目:初中数学 来源: 题型:
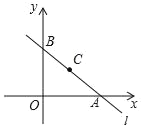
【题目】在平面直角坐标系xOy中,直线l与x轴,y轴分别交于A、B两点,且过点B(0,4)和C(2,2)两点.
(1)求直线l的解析式;
(2)求△AOB的面积;
(3)点P是x轴上一点,且满足△ABP为等腰三角形,直接写出所有满足条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某弹簧的长度与所挂物体质量之间的关系如下表:
所挂物体的质量/千克 | 0 | 1 | 2 | 3 | 4 | 5 |
弹簧的长度/厘米 | 10 | 10.4 | 10.8 | 11.2 | 11.6 | 12 |
(1)如果所挂物体的质量用x表示,弹簧的长度用y表示,请直接写出y与x满足的关系式.
(2)当所挂物体的质量为10千克时,弹簧的长度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB、AC的垂直平分线l1、l2相交于点O,若∠BAC等于82°,则∠OBC等于( )

A. 8°B. 9°C. 10°D. 11°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】主题班会课上,王老师出示了如图所示的一幅漫画,经过同学们的一番热议,达成以下四个观点:
A.放下自我,彼此尊重; B.放下利益,彼此平衡;
C.放下性格,彼此成就; D.合理竞争,合作双赢.
要求每人选取其中一个观点写出自己的感悟.根据同学们的选择情况,小明绘制了下面两幅不完整的图表,请根据图表中提供的信息,解答下列问题:


(1)参加本次讨论的学生共有 人;
(2)表中![]() ,
,![]() ;
;
(3)将条形统计图补充完整;
(4)现准备从![]() 四个观点中任选两个作为演讲主题,请用列表或画树状图的方法求选中观点
四个观点中任选两个作为演讲主题,请用列表或画树状图的方法求选中观点![]() (合理竞争,合作双赢)的概率.
(合理竞争,合作双赢)的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】早在1960年、中国登山队首次从珠穆朗玛北侧中国境内登上珠峰,近几十年,珠峰更是吸引了大批的登山爱好者,某日,登山运动员傅博准备从海拔7400米的3号营地登至海拔近7900米的4号营地,由于天气骤变,近6小时的攀爬过程中他不得不几次下撤躲避强高空风,记向上爬升的海拔高度为正数,向下撒退时下降的海拔高度为负数,傅博在这一天攀爬的海拔高度记录如下:(单位:米)+320、-55、+116、-20、+81、-43、+115.
(1)傳博能按原计划在这天登至4号营地吗?
(2)若在这一登山过程中,傅博所处位置的海拔高度上升或下降1米平均消耗8大卡的卡路里,则傅博这天消耗了多少卡路里?
(3)登山消耗的卡路里预估为:1千克身体重量(体重或负重)1天需要55~65(大于等于55,小于等于65)大卡的卡路里,海拔6000米以上会使卡路里消耗增加20%,登山协会约定海拔5000米以上运动员负重14千克,在(2)的条件下,请你估算傳博的体重范围.(精确到1千克)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com