Question

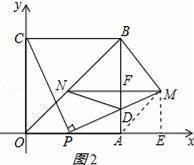
如图，四边形OABC是边长为4的正方形，点P为OA边上任意一点（与点O、A不重合），连接CP，过点P作PM⊥CP交AB于点D，且PM=CP，过点M作MN∥OA，交BO于点N，连接ND、BM，设OP=t．

（1）求点M的坐标（用含t的代数式表示）．

（2）试判断线段MN的长度是否随点P的位置的变化而改变？并说明理由．

（3）当t为何值时，四边形BNDM的面积最小．

　

Answer 1

【考点】四边形综合题．

【专题】压轴题．

【分析】（1）作ME⊥x轴于E，则∠MEP=90°，先证出∠PME=∠CPO，再证明△MPE≌△PCO，得出ME=PO=t，EP=OC=4，求出OE，即可得出点M的坐标；

（2）连接AM，先证明四边形AEMF是正方形，得出∠MAE=45°=∠BOA，AM∥OB，证出四边形OAMN是平行四边形，即可得出MN=OA=4；

（3）先证明△PAD∽△PEM，得出比例式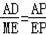，得出AD，求出BD，求出四边形BNDM的面积S是关于t的二次函数，即可得出结果．

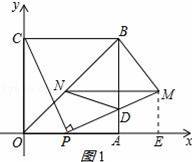
【解答】解：（1）作ME⊥x轴于E，如图1所示：

则∠MEP=90°，ME∥AB，

∴∠MPE+∠PME=90°，

∵四边形OABC是正方形，

∴∠POC=90°，OA=OC=AB=BC=4，∠BOA=45°，

∵PM⊥CP，

∴∠CPM=90°，

∴∠MPE+∠CPO=90°，

∴∠PME=∠CPO，

在△MPE和△PCO中，，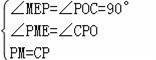

∴△MPE≌△PCO（AAS），

∴ME=PO=t，EP=OC=4，

∴OE=t+4，

∴点M的坐标为：（t+4，t）；

（2）线段MN的长度不发生改变；理由如下：

连接AM，如图2所示：

∵MN∥OA，ME∥AB，∠MEA=90°，

∴四边形AEMF是矩形，

又∵EP=OC=OA，

∴AE=PO=t=ME，

∴四边形AEMF是正方形，

∴∠MAE=45°=∠BOA，

∴AM∥OB，

∴四边形OAMN是平行四边形，

∴MN=OA=4；

（3）∵ME∥AB，

∴△PAD∽△PEM，

∴，

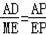
即，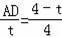

∴AD=﹣t²+t，

∴BD=AB﹣AD=4﹣（﹣t²+t）=t²﹣t+4，

∵MN∥OA，AB⊥OA，

∴MN⊥AB，

∴四边形BNDM的面积S=MN•BD=×4（t²﹣t+4）=（t﹣2）²+6，

∴S是t的二次函数，

∵＞0，

∴S有最小值，

当t=2时，S的值最小；

∴当t=2时，四边形BNDM的面积最小．

【点评】本题是四边形综合题目，考查了正方形的性质与判定、全等三角形的判定与性质、平行四边形的判定与性质、相似三角形的判定与性质、四边形面积的计算以及二次函数的最值等知识；本题难度较大，综合性强，特别是（2）（3）中，需要证明四边形是正方形、平行四边形、三角形相似以及运用二次函数才能得出结果．