
【题目】如图,甲、乙两动点分别从正方形![]() 的顶点
的顶点![]() 同时沿正方形的边开始移动,甲按顺时针方向环行,乙按逆时针方向环行,若乙的速度是甲的3倍,那么它们第1次相遇在边
同时沿正方形的边开始移动,甲按顺时针方向环行,乙按逆时针方向环行,若乙的速度是甲的3倍,那么它们第1次相遇在边![]() 上.
上.

(1)它们第2次相遇在边__________上;
(2)它们第2019次相遇在边__________上.
【答案】CD BC
【解析】
此题利用行程问题中的相遇问题,设出正方形的边长,乙的速度是甲的速度的3倍,求得每一次相遇的地点,找出规律即可解答.
设正方形的边长为![]() ,因为乙的速度是甲的速度的3倍,时间相同,甲乙所行的路程比为1:3,把正方形的每一条边平均分成2份,由题意知:
,因为乙的速度是甲的速度的3倍,时间相同,甲乙所行的路程比为1:3,把正方形的每一条边平均分成2份,由题意知:
第一次相遇甲乙行的路程和为2![]() ,
,
甲行的路程为2![]() ×
×![]() =
=![]() ,乙行的路程为2
,乙行的路程为2![]() ×
×![]() =
=![]() ,在AD边相遇;
,在AD边相遇;
②第二次相遇甲乙行的路程和为4![]() ,甲行的路程为4
,甲行的路程为4![]() ×
×![]() =
=![]() ,乙行的路程为4
,乙行的路程为4![]() ×
×![]() =3
=3![]() ,在CD边相遇;
,在CD边相遇;
第三次相遇甲乙行的路程和为4![]() ,甲行的路程为4
,甲行的路程为4![]() ×
×![]() =
=![]() ,乙行的路程为4
,乙行的路程为4![]() ×
×![]() =3
=3![]() ,在BC边相遇;
,在BC边相遇;
第四次相遇甲乙行的路程和为4![]() ,甲行的路程为4
,甲行的路程为4![]() ×
×![]() =
=![]() ,乙行的路程为4
,乙行的路程为4![]() ×
×![]() =3
=3![]() ,在AB边相遇;
,在AB边相遇;
第五次相遇甲乙行的路程和为4![]() ,甲行的路程为4
,甲行的路程为4![]() ×
×![]() =
=![]() ,乙行的路程为4
,乙行的路程为4![]() ×
×![]() =3
=3![]() ,在AD边相遇;
,在AD边相遇;
…
四次一个循环,因为2019=504×4+3,所以它们第2019次相遇在边BC上.
故答案为:CD;BC.


 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】在一次数学社团活动中,指导老师给同学们提出了以下问题:
问题:有67张卡片叠在一起,按从上而下的顺序先把第一张拿走,把第二张放到底层,然后把第三张拿走,再把第四张放到底层,如此进行下去,直至只剩最后一张卡片.问仅剩的这张卡片是原来的第几张卡片?
由于卡片数量较多,指导老师建议同学们先对较少的张数进行尝试,以便熟悉游戏规则并发现一些规律!
(1)请你试着在草稿纸上进行试验,将试验结果填写在下表中:
试验的卡片数量 (张) | 2 | 4 | 8 | 9 | 10 | 11 |
剩下最后一张卡片是 原来卡片的第几张 |
(2)根据试验结果的规律,回答最初的67张卡片情形,请你给出答案并简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C、D在线段BE上,下列说法:①直线CD上以B、C、D、E为端点的线段共有6条;②图中有2对互补的角;③若∠BAE=100°,∠DAC=40°,则以A为顶点的所有小于平角的角的度数和为360°;④若BC=2,CD=DE=3,点F是线段BE上任意一点,则点F到点B,C,D,E的距离之和的最大值为15,最小值为11.其中说法正确的个数有( )
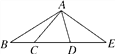
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=150,∠AOC=40,OE是∠AOB内部的一条射线,OF平分∠AOE, 且OF在OC的右侧.
(1)若∠EOB=10,求∠COF的度数;
(2)若∠COF=20,求∠EOB的度数;
(3)若∠COF=n,求∠EOB的度数(用含n的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线过原点O,点A(10,0)和点B(2,2),在线段OA上,点P从点O向点A运动,同时点Q从点A向点O运动,运动过程中保持AQ=2OP,当P、Q重合时同时停止运动,过点Q作x轴的垂线,交直线AB于点M,延长QM到点D,使MD=MQ,以QD为对角线作正方形QCDE(正方形QCDE随点Q运动).
(1)求这条抛物线的函数表达式;
(2)设正方形QCDE的面积为S,P点坐标(m,0)求S与m之间的函数关系式;
(3)过点P作x轴的垂线,交抛物线于点N,延长PN到点G,使NG=PN,以PG为对角线作正方形PFGH(正方形PFGH随点P运动),当点P运动到点(2,0)时,如图2,正方形PFGH的边GF和正方形QCDE的边EQ落在同一条直线上.
①则此时两个正方形中在直线AB下方的阴影部分面积的和是多少?
②若点P继续向点A运动,还存在两个正方形分别有边落在同一条直线上的情况,请直接写出每种情况下点P的坐标,不必说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列条件中,不能判断△ABC是直角三角形的是( )
A. a:b:c=3:4:5 B. ∠A:∠B:∠C=3:4:5
C. ∠A+∠B=∠C D. a:b:c=1:2:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】苏科版九年级下册数学课本91页有这样一道习题:


(1)复习时,小明与小亮、数学老师交流了自己的两个见解,并得到了老师的认可:
①可以假定正方形的边长AB=4a,则AE=DE=2a,DF=a,利用“两边分别成比例且夹角相等的两个三角形相似”可以证明△ABE∽△DEF;请结合提示写出证明过程.
②图中的相似三角形共三对,而且可以借助于△ABE与△DEF中的比例线段来证明△EBF与它们相似.证明过程如下:

(2)交流之后,小亮尝试对问题进行了变化,在老师的帮助下,提出了新的问题,请你解答:
已知:如图,在矩形ABCD中,E为AD的中点,EF⊥EC交AB于F,连结FC.
(AB>AE)

①求证:△AEF∽△ECF;
②设BC=2,AB=a,是否存在a值,使得△AEF与△BFC相似.若存在,请求出a的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com