
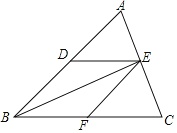
【题目】如图,在![]() 中,D、E、F分别是AB、AC、BC的中点,
中,D、E、F分别是AB、AC、BC的中点,
(1)求证:四边形DEFB是平行四边形;
(2)如果四边形DEFB是菱形,判断BE与AC的位置关系,并证明.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】山地自行车越来越受到中学生的喜爱,各种品牌相继投放市场,某车行经营的A型车去年销售总额为5万元,今年每辆销售价比去年降低400元,若卖出的数量相同,销售总额将比去年减少20%.
(1)今年A型车每辆售价多少元?(用列方程的方法解答)
(2)该车行计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?
A,B两种型号车的进货和销售价格如下表:
A型车 | B型车 | |
进货价格(元) | 1100 | 1400 |
销售价格(元) | 今年的销售价格 | 2000 |
查看答案和解析>>
科目:初中数学 来源: 题型:
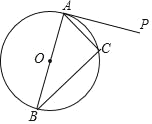
【题目】如图,△ABC为⊙O的内接三角形,其中AB为⊙O的直径,过点A作⊙O的切线PA.
(1)求证:∠PAC=∠ABC;
(2)若∠PAC=30°,AC=3,求劣弧AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
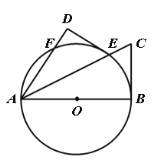
【题目】如图,已知AB是⊙O的直径,F是⊙O上一点,∠BAF的平分线交⊙O于点E,交⊙O的切线BC于点C,过点E作ED⊥AF,交AF的延长线于点D.
(1)求证:DE是⊙O的切线;
(2)若DE=3,CE=2,
①求![]() 值;
值;
②若点G 为AE上一点,求OG+![]() EG最小值.
EG最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
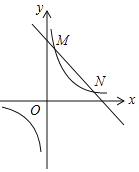
【题目】如图,一次函数y1=kx+b(k,b为常数,k≠0)的图象与反比例函数y2=![]() (m为常数,m≠0)的图象相交于点M(1,4)和点N(4,n).
(m为常数,m≠0)的图象相交于点M(1,4)和点N(4,n).
(1)反比例函数与一次函数的解析式.
(2)函数y2=![]() 的图象(x>0)上有一个动点C,若先将直线MN平移使它过点C,再绕点C旋转得到直线PQ,PQ交x轴于点A,交y轴点B,若BC=2CA,求OAOB的值.
的图象(x>0)上有一个动点C,若先将直线MN平移使它过点C,再绕点C旋转得到直线PQ,PQ交x轴于点A,交y轴点B,若BC=2CA,求OAOB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】猫眼专业版数据显示,截至北京时间2月10日21:00,选择在春节档上映的8部国产电影(《疯狂的外星人》、《飞驰人生》、《新喜剧之王》、《流浪地球》、《神探蒲松龄》《廉政风云》、《小猪佩奇过大年》、《熊出没原始时代》)总票房已经达到57.82亿元(含服务费),其中《流浪地球》居首.57.82亿用科学记数法表示为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10,以AB为直径的⊙O与BC交于点D,与AC交于点E,连OD交BE于点M,且MD=2.
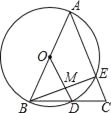
(1)求BE长;(2)求tanC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是某小区入口实景图,图2是该入口抽象成的平面示意图.已知入口BC宽3.9米,门卫室外墙AB上的O点处装有一盏路灯,点O与地面BC的距离为3.3米,灯臂OM长为1.2米(灯罩长度忽略不计),∠AOM=60°.
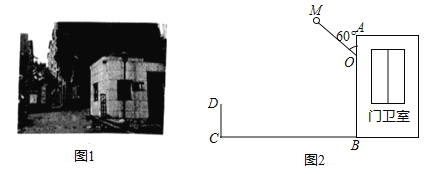
(1)求点M到地面的距离;
(2)某搬家公司一辆总宽2.55米,总高3.5米的货车从该入口进入时,货车需与护栏CD保持0.65米的安全距离,此时,货车能否安全通过?若能,请通过计算说明;若不能,请说明理由.(参考数据:![]() 1.73,结果精确到0.01米)
1.73,结果精确到0.01米)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com