

分析 (1)直接利用点B,C坐标,利用待定系数法求出函数解析即可;
(2)由AD=2CD,DE∥y轴,得出D,E两点的坐标,根据三角形的面积公式即可得出S与t之间的函数关系式,根据B,C两点坐标直接写出t的取值范围;
(3)假设抛物线上存在点P,使以点P、F、E、D为顶点的四边形为平行四边形,求出直线AC的解析式,设出点P坐标,从而得出点F坐标,整理出关于h的方程,求出P点坐标,使以点P、F、E、D为顶点的四边形为平行四边形.
解答 解:(1)把B(-1,0),C(3,0),代入函数解析式得:
$\left\{\begin{array}{l}{9a+3b+3=0}\\{a-b+3=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-1}\\{b=2}\end{array}\right.$
故抛物线解析式为:y=-x2+2x+3;
(2)设DE与x轴交于点H,
∵DE∥y轴,AD=2CD,
∴$\frac{DH}{OA}$=$\frac{CD}{AC}$=$\frac{1}{3}$,
∴DH=CH=1,
∴D(2,1),
∵点E在抛物线上,
∴E(2,3),
∵点P为x轴上方抛物线上的一点,设点P的横坐标为t,
∴-1<t<3,
∵△PDE的面积为S,
∴$\frac{1}{2}$DE•|t-2|=S,
∴S=|t-2|(-1<t<3),
即当-1<t<2时,S=2-t,
当2<t<3时,S=t-2;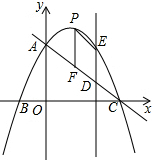
(3)如图所示:设直线AC的解析式为y=kx+b,
∴$\left\{\begin{array}{l}{b=3}\\{3k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=3}\\{k=-1}\end{array}\right.$,
∴直线AC的解析式为y=-x+3,
假设抛物线上存在点P,使以点P、F、E、D为顶点的四边形为平行四边形,
设点P坐标为(h,-h2+2h+3),
∵PF∥DE,
∴PF=DE,
∴F(h,-h+3),
∴-h2+2h+3-(-h+3)=2,
∴h2-3h+2=0,
∴h1=1,h2=2,
∴抛物线上存在点P,使以点P、F、E、D为顶点的四边形为平行四边形,点P的坐标为(1,4)或(2,3).
点评 本题主要考查了二次函数解析式的确定以及平行四边形的判定和性质等知识,要注意当情况不确定的情况下需要分类讨论,以免漏解.


科目:初中数学 来源: 题型:填空题
 如图,为了测量河的宽度AB,测量人员在高21m的建筑物CD的顶端D处测得河岸B处的俯角为45°,测得河对岸A处的俯角为30°(A,B,C在同一条直线上),则河的宽度AB约为15.3m.
如图,为了测量河的宽度AB,测量人员在高21m的建筑物CD的顶端D处测得河岸B处的俯角为45°,测得河对岸A处的俯角为30°(A,B,C在同一条直线上),则河的宽度AB约为15.3m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
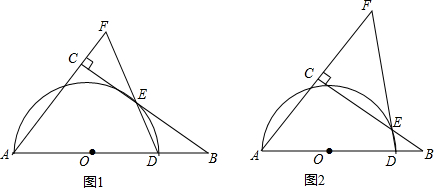
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com