
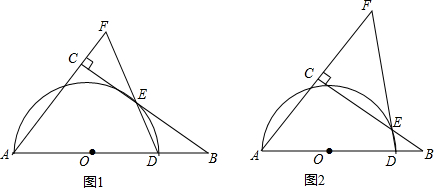
分析 (1)①如图1中,连接OE.只要证明OE∥AF,推出∠PED=∠F,由OE=OD,推出∠OED=∠ODE,推出∠F=∠ADF,即可推出AF=AD;
②在Rt△OBE中,sin∠B=$\frac{OE}{OB}$=$\frac{3}{5}$,设OE=3k,OB=5k,则BE=4k,由OE2+BE2=OB2,推出(3k)2+(4k)2=(3k+4)2,解得k=2或-$\frac{1}{2}$(舍弃),推出OE=OA=OD=6,OB=10,由OE∥AC,推出$\frac{OE}{AC}$=$\frac{BO}{BA}$,由此即可解决问题;
(2)如图2中,作DM⊥BC于M,连接AE.在Rt△ABC中,sin∠B=$\frac{AC}{AB}$=$\frac{3}{5}$.设AC=3a,AB=5a,则BC=4a,由EC=3EB,推出EC=3a,EB=a,设DM=x,推出AC=CE=3k,推出∠CAE=∠CEA=45°,易证EM=DM=x,BM=a-x由DM∥AC,推出$\frac{DM}{AC}$=$\frac{BM}{BC}$,可得$\frac{x}{3a}$=$\frac{a-x}{4a}$,推出x=$\frac{3}{7}$a,求出△CEF,四边形ADEC,△DEB的面积(用a表示)即可解决问题:
解答 (1)①证明:如图1中,连接OE.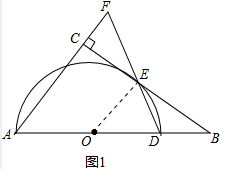
∵BC是⊙O的切线,
∴OE⊥BC,
∵AC⊥BC,
∴OE∥AF,
∴∠PED=∠F,
∵OE=OD,
∴∠OED=∠ODE,
∴∠F=∠ADF,
∴AF=AD.
②解:在Rt△OBE中,sin∠B=$\frac{OE}{OB}$=$\frac{3}{5}$,设OE=3k,OB=5k,则BE=4k,
∵OE2+BE2=OB2,
∴(3k)2+(4k)2=(3k+4)2,
解得k=2或-$\frac{1}{2}$(舍弃),
∴OE=OA=OD=6,OB=10,
∵OE∥AC,
∴$\frac{OE}{AC}$=$\frac{BO}{BA}$,
∴$\frac{6}{AC}$=$\frac{10}{16}$,
∴AC=$\frac{48}{5}$.
(2)解:如图2中,作DM⊥BC于M,连接AE.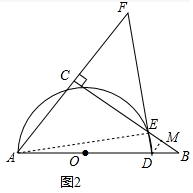
在Rt△ABC中,sin∠B=$\frac{AC}{AB}$=$\frac{3}{5}$.设AC=3a,AB=5a,则BC=4a,
∵EC=3EB,
∴EC=3a,EB=a,设DM=x,
∴AC=CE=3k,
∴∠CAE=∠CEA=45°,
∵AD是直径,
∴∠AED=∠AEF=90°,
∴∠CEF=∠DEM=45°,
∴EM=DM=x,BM=a-x
∵DM∥AC,
∴$\frac{DM}{AC}$=$\frac{BM}{BC}$,
∴$\frac{x}{3a}$=$\frac{a-x}{4a}$,
∴x=$\frac{3}{7}$a,
∴AC=CE=CF=3a,AE=3$\sqrt{2}$a,DE=$\frac{3}{7}$$\sqrt{2}$a,
∴S△EDF=$\frac{1}{2}$×3a×3a=$\frac{9}{2}$a2,
S四边形ADEC=S△ACE+S△AED=$\frac{9}{2}$a2+$\frac{1}{2}$•3$\sqrt{2}$a•$\frac{3\sqrt{2}}{7}$a=$\frac{81}{14}$a2,
S△BDE=$\frac{1}{2}$×a×$\frac{3}{7}$a=$\frac{3}{14}$a2,
∴S△CEF:S四边形ADEC:S△BDE=$\frac{9}{2}$a2:$\frac{81}{14}$a2:$\frac{3}{14}$a2=21:27:1.
故答案为21:27:1.
点评 本题考查圆综合题、切线的性质、勾股定理、锐角三角函数、平行线等分线段定理等知识,解题的关键是灵活运用所学知识解决问题,学会利用参数解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
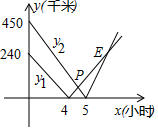 高速公路上依次有3个标志点A、B、C,甲、乙两车分别从A、C两点同时出发,匀速行驶,甲车从A→B→C,乙车从C→B→A,甲、乙两车离B的距离y1、y2(千米)与行驶时间x(小时)之间的函数关系图象如图所示.观察图象,给出下列结论:①A、C之间的路程为690千米;②乙车比甲车每小时快30千米;③4.5小时两车相遇;④点E的坐标为(7,180),其中正确的有①②④(把所有正确结论的序号都填在横线上).
高速公路上依次有3个标志点A、B、C,甲、乙两车分别从A、C两点同时出发,匀速行驶,甲车从A→B→C,乙车从C→B→A,甲、乙两车离B的距离y1、y2(千米)与行驶时间x(小时)之间的函数关系图象如图所示.观察图象,给出下列结论:①A、C之间的路程为690千米;②乙车比甲车每小时快30千米;③4.5小时两车相遇;④点E的坐标为(7,180),其中正确的有①②④(把所有正确结论的序号都填在横线上).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
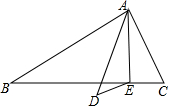 如图,已知△ABC,∠B=30°,∠C=60°,AC=2,E是BC边上一点,将△AEC沿AE翻折,点C落在点D处,若DE∥AB,则EC=4-2$\sqrt{3}$.
如图,已知△ABC,∠B=30°,∠C=60°,AC=2,E是BC边上一点,将△AEC沿AE翻折,点C落在点D处,若DE∥AB,则EC=4-2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知,点A的坐标是(-1,-3),点B的坐标是(-3,-2),点C的坐标是(-3,-3)
已知,点A的坐标是(-1,-3),点B的坐标是(-3,-2),点C的坐标是(-3,-3)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com