
 如图,为了测量河的宽度AB,测量人员在高21m的建筑物CD的顶端D处测得河岸B处的俯角为45°,测得河对岸A处的俯角为30°(A,B,C在同一条直线上),则河的宽度AB约为15.3m.
如图,为了测量河的宽度AB,测量人员在高21m的建筑物CD的顶端D处测得河岸B处的俯角为45°,测得河对岸A处的俯角为30°(A,B,C在同一条直线上),则河的宽度AB约为15.3m. 分析 在Rt△ACD中,根据已知条件求出AC的值,再在Rt△BCD中,根据∠EDB=45°,求出BC=CD=21m,最后根据AB=AC-BC,代值计算即可.
解答 解:∵在Rt△ACD中,CD=21m,∠DAC=30°,
∴AC=$\frac{CD}{tan30°}$=$\frac{21}{\frac{\sqrt{3}}{3}}$=21$\sqrt{3}$m,
在Rt△BCD中,
∵∠EDB=45°,
∴∠DBC=45°,
∴BC=CD=21m,
∴AB=AC-BC=21$\sqrt{3}$-21≈15.3(m),
∴河的宽度AB约是15.3m.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,熟记锐角三角函数的定义是解答此题的关键.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:解答题
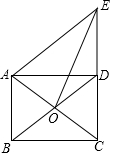 如图,矩形ABCD的对角线AC,BD相交于点O,过点A作BD的平行线交CD的延长线于点E.
如图,矩形ABCD的对角线AC,BD相交于点O,过点A作BD的平行线交CD的延长线于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
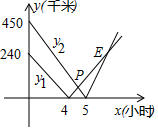 高速公路上依次有3个标志点A、B、C,甲、乙两车分别从A、C两点同时出发,匀速行驶,甲车从A→B→C,乙车从C→B→A,甲、乙两车离B的距离y1、y2(千米)与行驶时间x(小时)之间的函数关系图象如图所示.观察图象,给出下列结论:①A、C之间的路程为690千米;②乙车比甲车每小时快30千米;③4.5小时两车相遇;④点E的坐标为(7,180),其中正确的有①②④(把所有正确结论的序号都填在横线上).
高速公路上依次有3个标志点A、B、C,甲、乙两车分别从A、C两点同时出发,匀速行驶,甲车从A→B→C,乙车从C→B→A,甲、乙两车离B的距离y1、y2(千米)与行驶时间x(小时)之间的函数关系图象如图所示.观察图象,给出下列结论:①A、C之间的路程为690千米;②乙车比甲车每小时快30千米;③4.5小时两车相遇;④点E的坐标为(7,180),其中正确的有①②④(把所有正确结论的序号都填在横线上).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
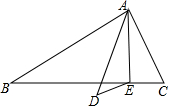 如图,已知△ABC,∠B=30°,∠C=60°,AC=2,E是BC边上一点,将△AEC沿AE翻折,点C落在点D处,若DE∥AB,则EC=4-2$\sqrt{3}$.
如图,已知△ABC,∠B=30°,∠C=60°,AC=2,E是BC边上一点,将△AEC沿AE翻折,点C落在点D处,若DE∥AB,则EC=4-2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某市中考体育测试有“跳绳”项目,为加强训练,某班女生分成甲、乙两组参加班级跳绳对抗赛,两组参赛人数相等,比赛结束后,依据两组学生的成绩(满分为10分)绘制了如下统计图表:
某市中考体育测试有“跳绳”项目,为加强训练,某班女生分成甲、乙两组参加班级跳绳对抗赛,两组参赛人数相等,比赛结束后,依据两组学生的成绩(满分为10分)绘制了如下统计图表:| 分 数 | 人 数 |
| 5分 | 5人 |
| 6分 | 2人 |
| 7分 | 3人 |
| 8分 | 1人 |
| 9分 | 4人 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com