
【题目】如图,已知矩形ABCD中,AB=4,AD=m,动点P从点D出发,在边DA上以每秒1个单位的速度向点A运动,连接CP,作点D关于直线PC的对称点E,设点P的运动时间为t(s).
(1)若m=6,求当P,E,B三点在同一直线上时对应的t的值.
(2)已知m满足:在动点P从点D到点A的整个运动过程中,有且只有一个时刻t,使点E到直线BC的距离等于3,求所有这样的m的取值范围.

【答案】(1) ![]() ;(2)
;(2) ![]() ≤m<4
≤m<4![]() .
.
【解析】
试题分析:(1)只要证明△ABD∽△DPC,可得![]() ,由此求出PD即可解决问题;
,由此求出PD即可解决问题;
(2)分两种情形求出AD的值即可解决问题:①如图2中,当点P与A重合时,点E在BC的下方,点E到BC的距离为3.②如图3中,当点P与A重合时,点E在BC的上方,点E到BC的距离为3
试题解析:(1)如图1中,
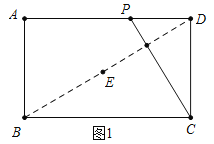
∵四边形ABCD是矩形,
∴∠ADC=∠A=90°,
∴∠DCP+∠CPD=90°,
∵∠CPD+∠ADB=90°,
∴∠ADB=∠PCD,
∵∠A=∠CDP=90°,
∴△ABD∽△DPC,
∴![]() ,
,
∴![]() ,
,
∴PD=![]() ,
,
∴t=![]() s时,B、E、D共线.
s时,B、E、D共线.
(2)如图2中,当点P与A重合时,点E在BC的下方,点E到BC的距离为3.
作EQ⊥BC于Q,EM⊥DC于M.则EQ=3,CE=DC=4
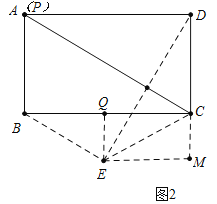
易证四边形EMCQ是矩形,
∴CM=EQ=3,∠M=90°,
∴EM=![]() ,
,
∵∠DAC=∠EDM,∠ADC=∠M,
∴△ADC∽△DME,
![]() ,
,
∴![]() ,
,
∴AD=4![]() ,
,
如图3中,当点P与A重合时,点E在BC的上方,点E到BC的距离为3.
作EQ⊥BC于Q,延长QE交AD于M.则EQ=3,CE=DC=4
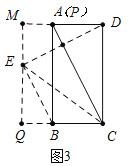
在Rt△ECQ中,QC=DM=![]() ,
,
由△DME∽△CDA,
∴![]() ,
,
∴![]() ,
,
∴AD=![]() ,
,
综上所述,在动点P从点D到点A的整个运动过程中,有且只有一个时刻t,使点E到直线BC的距离等于3,这样的m的取值范围![]() ≤m<4
≤m<4![]() .
.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
【题目】如果二次函数![]() 的图象与
的图象与![]() 轴有两个公共点,那么一元二次方程
轴有两个公共点,那么一元二次方程![]() 有两个不相等的实根,请根据你对这句话的理解,解决下列问题:若
有两个不相等的实根,请根据你对这句话的理解,解决下列问题:若![]() 、
、![]() (
(![]() <
<![]() )是关于的方程
)是关于的方程![]() 的两根,且
的两根,且![]() <
<![]() 则
则![]() 、
、![]() 、
、![]() 、
、![]() 的大小关系是( )
的大小关系是( )
A. ![]() <
<![]() <
<![]() <
<![]() B.
B. ![]() <
<![]() <
<![]() <
<![]()
C. ![]() <
<![]() <
<![]() <
<![]() D.
D. ![]() <
<![]() <
<![]() <
<![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
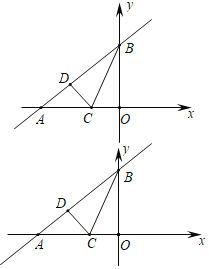
【题目】已知:直线y=![]() x+3与x轴、y轴分别相于点A和点B,点C在线段AO上.
x+3与x轴、y轴分别相于点A和点B,点C在线段AO上.
将△CBO沿BC折叠后,点O恰好落在AB边上点D处
(1)求直线BC的解析式;
(2)求点D的坐标;
(3)P为平面内一动点,且以A、B、C、P为顶点的四边形为平行四边形,直接写出点P坐标 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:如图,在Rt△ABC中,∠ACB=90°∠BAC=30°.
动手操作:(1)若以直角边AC所在的直线为对称轴.将Rt△ABC作轴对称变换,请你在原图上作出它的对称图形:
观察发现:(2)Rt△ABC和它的对称图形组成了什么图形?你最准确的判断是 .
合作交流:(3)根据上面的图形,请你猜想直角边BC与斜边AB的数量关系,并证明你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为地铁调价后的计价表.调价后小明、小伟从家到学校乘地铁分别需要4元和3元.由于刷卡坐地铁有优惠,因此,他们平均每次实付3.6元和2.9元.已知小明从家到学校乘地铁的里程比小伟从家到学校的里程多5 km,且小明每千米享受的优惠金额是小伟的2倍,求小明和小伟从家到学校乘地铁的里程分别是多少千米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的圆交AC于点D,交BC于点E,延长AE至点F,使EF=AE,连接FB,FC.
(1)求证:四边形ABFC是菱形;
(2)若AD=7,BE=2,求半圆和菱形ABFC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是等边三角形ABC外接圆⊙O上的点,在以下判断中,不正确的是

A、当弦PB最长时,ΔAPC是等腰三角形 B、当ΔAPC是等腰三角形时,PO⊥AC
C、当PO⊥AC时,∠ACP=300 D、当∠ACP=300时,ΔPBC是直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面的图象反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后又原路返回,顺路到文具店去买笔,然后散步回家.其中x表示时间,y表示张强离家的距离.根据图象回答:
(1)体育场离张强家的多远?张强从家到体育场用了多长时间?
(2)体育场离文具店多远?
(3)张强在文具店逗留了多久?
(4)计算张强从文具店回家的平均速度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com