
分析 (1)由2×4×6×8+16=16×(22+1)2=400,4×6×8×10+16=16×(32+2)2=1936,6×8×10×12+16=16×(42+3)2=5776,…;
(2)由(1)中的计算得出四个连续偶数的乘积加上16等于序数加1的平方与1的和的平方的16倍;
(3)由(2)的规律用式子表示为2n(2n+2)(2n+4)(2n+6)+16=16[(n+1)2+n]2;进一步验证即可.
解答 解:(1)2×4×6×8+16=16×(22+1)2=400,
4×6×8×10+16=16×(32+2)2=1936,
6×8×10×12+16=16×(42+3)2=5776,
…;
(2)从上面的计算过程中,可以发现四个连续偶数的乘积加上16等于序数加1的平方再加上1的和的平方的16倍;
(3)2n(2n+2)(2n+4)(2n+6)+16=16×[(n+1)2+n]2;
理由:左边=2n(2n+2)(2n+4)(2n+6)+16
=16[(n2+3n)(n2+3n+2)+1]
=16[(n+1)2+n]2;
右边=16[(n+1)2+n]2;
左边=右边
所以2n(2n+2)(2n+4)(2n+6)+16=16×[(n+1)2+n]2.
点评 此题考查数字的变化规律,找出数字之间的运算规律,利用规律解决问题.


科目:初中数学 来源: 题型:解答题
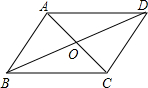 如图,在?ABCD中,对角线AC,BD相交于点O,若BD与AC的和为18cm,CD:DA=2:3,△AOB的周长为13cm,求BC的长.
如图,在?ABCD中,对角线AC,BD相交于点O,若BD与AC的和为18cm,CD:DA=2:3,△AOB的周长为13cm,求BC的长.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
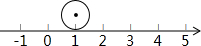 如图,把半径等于$\frac{1}{2}$的圆放到数轴上,圆上一点A与表示1的点重合,圆沿着数轴滚动一周,此时点A表示的数是1-π或1+π..
如图,把半径等于$\frac{1}{2}$的圆放到数轴上,圆上一点A与表示1的点重合,圆沿着数轴滚动一周,此时点A表示的数是1-π或1+π..查看答案和解析>>
科目:初中数学 来源: 题型:解答题
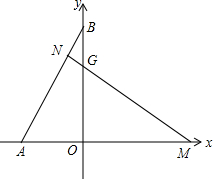 在平面直角坐标中,x轴上有点A和点M,y轴上有一点B,过点M作MN⊥AB于点N,交y轴于点G,且MG=AB,OA、OM(OA<OM)的长是方程x2-7x+12=0的两个根.
在平面直角坐标中,x轴上有点A和点M,y轴上有一点B,过点M作MN⊥AB于点N,交y轴于点G,且MG=AB,OA、OM(OA<OM)的长是方程x2-7x+12=0的两个根.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2.16×108人 | B. | 2.16×107人 | C. | 0.216×108人 | D. | 216×105人 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com