
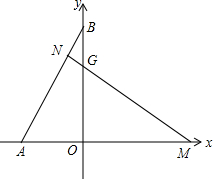
 在平面直角坐标中,x轴上有点A和点M,y轴上有一点B,过点M作MN⊥AB于点N,交y轴于点G,且MG=AB,OA、OM(OA<OM)的长是方程x2-7x+12=0的两个根.
在平面直角坐标中,x轴上有点A和点M,y轴上有一点B,过点M作MN⊥AB于点N,交y轴于点G,且MG=AB,OA、OM(OA<OM)的长是方程x2-7x+12=0的两个根.分析 (1)由一对直角相等,一对对顶角相等得到三角形BNG与三角形OMG相似,利用相似三角形对应角相等得到∠ABO=∠OMG,再由一对直角相等,AB=MG,利用AAS得到三角形AOB与三角形OMG全等,利用全等三角形对应边相等得到OB=OM,OG=OA,求出已知方程的解确定出OA与OM的长,求出A与M坐标,进而确定出B的坐标即可;
(2)由(1)确定出G与M坐标,设直线MN解析式为y=kx+b,把G与M坐标代入求出k与b的值,确定出直线MN解析式即可;
(3)直线MN上存在点P,△PMA是等腰三角形,如图所示,分三种情况考虑:若PA=PM;MP=MA;AM=PM,分别求出P的坐标即可.
解答 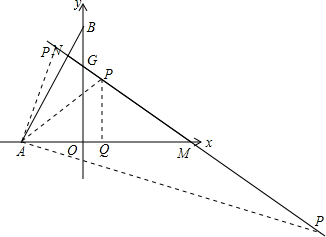 解:(1)∵∠BNG=∠GOM=90°,∠BGN=∠MGO,
解:(1)∵∠BNG=∠GOM=90°,∠BGN=∠MGO,
∴∠BNG=∠OMG,
在△AOB和△GOM中,
$\left\{\begin{array}{l}{∠ABO=∠GMO}\\{∠AOB=∠GOM}\\{AB=MG}\end{array}\right.$,
∴△AOB≌△GOM(AAS),
∴OB=OM,OA=OG,
方程x2-7x+12=0,
分解因式得:(x-3)(x-4)=0,
解得:x=3或x=4,
∴OA=3,OM=4,
∴A(-3,0),M(4,0),B(0,4);
(2)由(1)得:G(0,3),M(4,0),
设直线MN解析式为y=kx+b,
把G与M坐标代入得:$\left\{\begin{array}{l}{b=3}\\{4k+b=0}\end{array}\right.$,
解得:k=-$\frac{3}{4}$,b=3,
则直线MN解析式为y=-$\frac{3}{4}$x+3;
(3)直线MN上存在点P,△PMA是等腰三角形,
分三种情况考虑:若PA=PM,作PQ⊥AM,可得PQ垂直平分AM,
由A(-3,0),M(4,0),得到AM=7,即QM=$\frac{7}{2}$,OQ=4-$\frac{7}{2}$=$\frac{1}{2}$,
把x=$\frac{1}{2}$代入得:y=$\frac{21}{8}$,此时P($\frac{1}{2}$,$\frac{21}{8}$);
若AM=MP,设P(a,-$\frac{3}{4}$a+3),由M(4,0),
得到(a-4)2+(-$\frac{3}{4}$a+3)2=49,
解得:a=$\frac{48}{5}$或a=-$\frac{8}{5}$,
此时P($\frac{48}{5}$,-$\frac{21}{5}$),P(-$\frac{8}{5}$,$\frac{21}{5}$),
综上,满足题意P的坐标为($\frac{1}{2}$,$\frac{21}{8}$)或($\frac{48}{5}$,-$\frac{21}{5}$)或(-$\frac{8}{5}$,$\frac{21}{5}$).
点评 此题属于一次函数解析式,涉及的知识有:全等三角形的判定与性质,一元二次方程的解法,坐标与图形性质,待定系数法求一次函数解析式,熟练掌握待定系数法是解本题第二问的关键.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:解答题
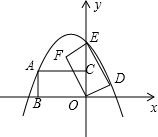 如图所示,在平面直角坐标系中,矩形ODEF的对角线OE在y轴上,将矩形ODEF横坐标原点O按逆时针方向旋转60°后,得到矩形OCAB,点E的对应点为点A,点F的对应点为x轴上点B,已知抛物线y=ax2+bx+2经过点A、D、E三点.
如图所示,在平面直角坐标系中,矩形ODEF的对角线OE在y轴上,将矩形ODEF横坐标原点O按逆时针方向旋转60°后,得到矩形OCAB,点E的对应点为点A,点F的对应点为x轴上点B,已知抛物线y=ax2+bx+2经过点A、D、E三点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 6 | C. | 9 | D. | 19 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 甲、乙两位同学的成绩一样稳定 | B. | 甲同学的成绩更稳定 | ||
| C. | 乙同学的成绩更稳定 | D. | 两位同学的成绩的稳定性不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com