
【题目】如图,在△ABC中,D、E、F分别是各边的中点,BH是AC边上的高.

(1)求证:四边形DBEF是平行四边形;(2)求证:∠DFE=∠DHE.
【答案】(1)见解析;(2)见解析.
【解析】
(1)根据三角形中位线定理得到DF∥BC,EF∥AB,于是得到结论;
(2)根据平行线的性质得到∠A=∠EFH,再在Rt△ABH中利用直角三角形斜边上的中线等于斜边一半的性质得到DA=DH,于是∠EFH=∠FHD,同理,∠CHE=∠AFD,根据平角的定义即可得到结论.
证明:(1)∵D、E、F分别是各边的中点,
∴DF和EF是△ABC的中位线,
∴DF∥BC,EF∥AB,
∴DF∥BE,EF∥BD,
∴四边形DBEF是平行四边形;
(2)∵EF∥AB,∴∠A=∠EFH,
∵BH⊥AC,∴∠AHB=90°,
∵D为AB的中点,
∴AD=DH,
∴∠AHD=∠A,
∴∠EFH=∠FHD,
同理,∠CHE=∠AFD,
∴∠DFE=∠DHE.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
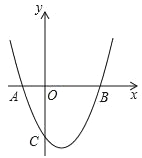
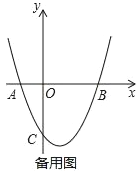
【题目】在平面直角坐标系xOy中,抛物线y=x2+bx+c与x轴交于点A,B(A在B的左侧),抛物线的对称轴为直线x=1,AB=4.
(1)求抛物线的表达式;
(2)抛物线上有两点M(x1,y1)和N(x2,y2),若x1<1,x2>1,x1+x2>2,试判断y1与y2的大小,并说明理由;
(3)平移该抛物线,使平移后的抛物线经过点O,且与x轴交于点D,记平移后的抛物线顶点为点P
①若△ODP是等腰直角三角形,求点P的坐标;
②在①的条件下,直线x=m(0<m<3)分别交线段BP、BC于点E、F,且△BEF的面积:△BPC的面积=2:3,直接写出m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题再现:
数形结合是一种重要的数学思想方法,借助这种思想方法可将抽象的数学知识变得直观并且具有可操作性.初中数学里的一些代数公式,很多都可以通过表示几何图形面积的方法进行直观推导和解释.
例如:利用图形的几何意义验证完全平方公式.
将一个边长为![]() 的正方形的边长增加
的正方形的边长增加![]() ,形成两个长方形和两个正方形,如图所示:这个图形的面积可以表示成:
,形成两个长方形和两个正方形,如图所示:这个图形的面积可以表示成:
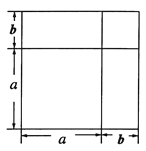
![]() 或
或![]()
∴![]()
这就验证了两数和的完全平方公式.
类比解决:
请你类比上述方法,利用图形的几何意义验证平方差公式.
(要求画出图形并写出推理过程)
问题提出:如何利用图形几何意义的方法证明![]() ?
?
如图所示,![]() 表示1个1×1的正方形,即:
表示1个1×1的正方形,即:![]() ,
,![]() 表示1个2×2的正方形,
表示1个2×2的正方形,![]() 与
与![]() 恰好可以拼成1个2×2的正方形,因此:
恰好可以拼成1个2×2的正方形,因此:![]() 、
、![]() 、
、![]() 就可以表示2个2×2的正方形,即:
就可以表示2个2×2的正方形,即:![]() 而
而![]() 、
、![]() 、
、![]() 、
、![]() 恰好可以拼成一个
恰好可以拼成一个![]() 的大正方形.
的大正方形.
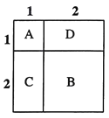
由此可得:![]() .
.
尝试解决:
请你类比上述推导过程,利用图形的几何意义确定:![]() _______.(要求写出结论并构造图形写出推证过程).
_______.(要求写出结论并构造图形写出推证过程).
问题拓广:
请用上面的表示几何图形面积的方法探究:![]() _______.(直接写出结论即可,不必写出解题过程).
_______.(直接写出结论即可,不必写出解题过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y1=k1x+b的图象与x轴、y轴分别交于A、B两点,与反比例函数![]() 的图象分别交于C、D两点,点D(2,﹣3),点B是线段AD的中点.
的图象分别交于C、D两点,点D(2,﹣3),点B是线段AD的中点.
(1)求一次函数y1=k1x+b与反比例函数![]() 的解析式;
的解析式;
(2)求△COD的面积;
(3)直接写出y1>y2时自变量x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把正方形纸片对折得到矩形ABCD,点E在BC上,把△ECD沿ED折叠,使点C恰好落在AD上点C′处,点M、N分别是线段AC′与线段BE上的点,把四边形ABNM沿NM向下翻折,点A落在DE的中点A′处.若原正方形的边长为12,则线段MN的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果关于![]() 的不等式组
的不等式组![]() 的整数解仅有
的整数解仅有![]() ,
,![]() ,那么适合这个不等式组的整数
,那么适合这个不等式组的整数![]() ,
,![]() 组成的有序数对
组成的有序数对![]() 共有_______个;如果关于
共有_______个;如果关于![]() 的不等式组
的不等式组![]() (其中
(其中![]() ,
,![]() 为正整数)的整数解仅有
为正整数)的整数解仅有![]() ,那么适合这个不等式组的整数
,那么适合这个不等式组的整数![]() ,
,![]() 组成的有序数对
组成的有序数对![]() 共有______个.(请用含
共有______个.(请用含![]() 、
、![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
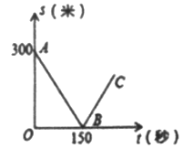
【题目】甲、乙两名自行车爱好者准备在段长为3500米的笔直公路上进行比赛,比赛开始时乙在起点,甲在乙的前面.他们同时出发,匀速前进,已知甲的速度为12米/秒,设甲、乙两人之间的距离为s(米),比赛时间为t(秒),图中的折线表示从两人出发至其中一人先到达终点的过程中s(米)与t(秒)的函数关系根据图中信息,回答下列问题:
(1)乙的速度为多少米/秒;
(2)当乙追上甲时,求乙距起点多少米;
(3)求线段BC所在直线的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.
(1)证明:四边形ACDE是平行四边形;
(2)若AC=8,BD=6,求平行四边形ACDE的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com