
【题目】如图,正方形ABCD绕点B逆时针旋转30°后得到正方形BEFG,EF与AD相交于点H,延长DA交GF于点K.若正方形ABCD边长为 ![]() ,则AK= .
,则AK= . 
【答案】2 ![]() ﹣3
﹣3
【解析】解:连接BH,如图所示:
∵四边形ABCD和四边形BEFG是正方形,
∴∠BAH=∠ABC=∠BEH=∠F=90°,
由旋转的性质得:AB=EB,∠CBE=30°,
∴∠ABE=60°,
在Rt△ABH和Rt△EBH中,![]() ,
,
∴Rt△ABH≌△Rt△EBH(HL),
∴∠ABH=∠EBH= ![]() ∠ABE=30°,AH=EH,
∠ABE=30°,AH=EH,
∴AH=ABtan∠ABH= ![]() ×
× ![]() =1,
=1,
∴EH=1,
∴FH= ![]() ﹣1,
﹣1,
在Rt△FKH中,∠FKH=30°,
∴KH=2FH=2( ![]() ﹣1),
﹣1),
∴AK=KH﹣AH=2( ![]() ﹣1)﹣1=2
﹣1)﹣1=2 ![]() ﹣3;
﹣3;
故答案为:2 ![]() ﹣3.
﹣3.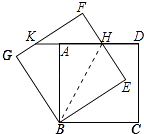
连接BH,由正方形的性质得出∠BAH=∠ABC=∠BEH=∠F=90°,由旋转的性质得:AB=EB,∠CBE=30°,得出∠ABE=60°,由HL证明Rt△ABH≌Rt△EBH,得出∠ABH=∠EBH= ![]() ∠ABE=30°,AH=EH,由三角函数求出AH,得出EH、FH,再求出KH=2FH,即可求出AK.
∠ABE=30°,AH=EH,由三角函数求出AH,得出EH、FH,再求出KH=2FH,即可求出AK.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:
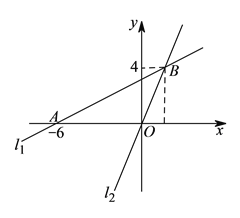
【题目】如图,在平面直角坐标系![]() 中,过点
中,过点![]() 的直线
的直线![]() 与直线
与直线![]() ;
;![]() 相交于点
相交于点![]() .
.
(![]() )求直线
)求直线![]() 的表达式.
的表达式.
(![]() )过动点
)过动点![]() 且垂于
且垂于![]() 轴的直线与
轴的直线与![]() 、
、![]() 的交点分别为
的交点分别为![]() ,
,![]() ,当点
,当点![]() 位于点
位于点![]() 上方时,写出
上方时,写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在Rt△ABC中,∠C=90°,BC=6cm,AC=8 cm,AB=10 cm. 现有一动点P,从A点出发,沿着三角形的边AC-CB-BA运动,回到A点停止,速度为1 cm/s,设运动时间为t s.
(1)当t=_______时,△ABC的周长被线段AP平分为相等的两部分.
(2)当t=_______时,△APC的面积等于△ABC面积的一半.
(3)还有一个△DEF,∠E=90°,如图②所示,DE=4cm,DF=5cm,∠D=∠A. 在△ABC的边上,若另外有一个动点Q,与P 同时从A点出发,沿着边AB-BC-CA运动,回到点A停止. 在两点运动过程中某一时刻,恰好△APQ与△DEF全等,则点Q的运动速度 cm/s.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,正确的有( )
①Rt△ABC中,已知两边长分别为3和4,则第三边长为5;
②有一个内角等于其他两个内角和的三角形是直角三角形;
③三角形的三边分别为a,b,C,若a2+c2=b2,那么∠C=90°;
④若△ABC中,∠A:∠B:∠C=1:5:6,则△ABC是直角三角形.
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某市近郊有一块长为60米,宽为50米的矩形荒地,地方政府准备在此建一个综合性休闲广场,其中阴影部分为通道,通道的宽度均相等,中间的三个矩形(其中三个矩形的一边长均为a米)区域将铺设塑胶地面作为运动场地. 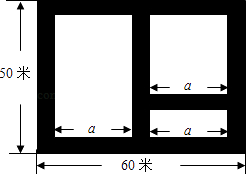
(1)设通道的宽度为x米,则a=(用含x的代数式表示);
(2)若塑胶运动场地总占地面积为2430平方米.请问通道的宽度为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
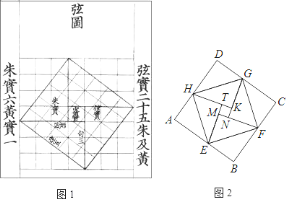
【题目】我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”(如图![]() ),图
),图![]() 由弦图变化得到,它是由作个全等的直角三角形拼接而成,记图中正方形
由弦图变化得到,它是由作个全等的直角三角形拼接而成,记图中正方形![]() ,正方形
,正方形![]() ,正方形
,正方形![]() 的面积分别为
的面积分别为![]() 、
、![]() 、
、![]() ,若
,若![]() ,则
,则![]() 的值是( )
的值是( )
A. 5 B. ![]() C.
C. ![]() D. 4
D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ACD和△BCE中,AC=BC,AD=BE,CD=CE,∠ACE=55°,∠BCD=155°,AD与BE相交于点P,则∠BPD的度数为( )
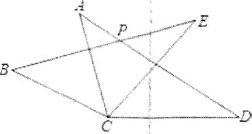
A. 120° B. 125° C. 130° D. 155°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com