Question

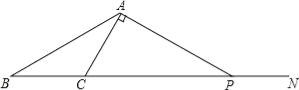
【题目】如图，点N是△ABC的边BC延长线上的一点，∠ACN=2∠BAC，过点A作AC的垂线交CN于点P．

（1）若∠APC=30°，求证：AB=AP；

（2）若AP=8，BP=16，求AC的长；

（3）若点P在BC的延长线上运动，∠APB的平分线交AB于点M．你认为∠AMP的大小是否发生变化？若变化，请说明理由；若不变化，求出∠AMP的大小．

Answer 1

【答案】(1)、证明过程见解析；(2)、6；(3)、45°.

【解析】

试题分析：(1)、由∠P=30°，∠CAP=90°得∠ACP=60°，∠BAC=30°，所以∠ABP=30°，进而可得∠ABP=∠P，即AB=AP；(2)、设AC=x，由勾股定理建立方程得x2+82=（16﹣x）2求出x的值即可求出AC的长；

(3)、∠AMP的大小不发生变化，由∠AMP=∠B+∠APC=∠ACP+∠APC=（∠ACP+∠APC）=90°=45°进而可得结论．

试题解析：(1)、∵AC⊥AP， ∴∠CAP=90°， ∵∠P=30°， ∴∠ACP=60°， ∴∠BAC=30°，

∴∠ABP=30°， ∴∠ABP=∠P， ∴AB=AP；

(2)、设AC=x，在Rt△ACP中，由勾股定理建立方程得x2+82=（16﹣x）2 解得x=6， 所以AC=6；

(3)、∠AMP的大小不发生变化

理由如下： ∵∠AMP=∠B+∠APC=∠ACP+∠APC=（∠ACP+∠APC）=90°=45°，

∴是一个的值，即不发生变化．