
【题目】如图,点C在线段AB上,AC=16cm,CB=12cm,点M、N分别是AC、BC的中点.![]()
(1)求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB=a cm,其它条件不变,你能猜想MN的长度吗?并说明理由.
(3)若C在线段AB的延长线上,且满足AC﹣BC=b cm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,不要说明理由.
【答案】
(1)解:∵点M、N分别是AC、BC的中点,
∴MC= ![]() AC=
AC= ![]() ×8cm=4cm,NC=
×8cm=4cm,NC= ![]() BC=
BC= ![]() ×6cm=3cm,
×6cm=3cm,
∴MN=MC+NC=4cm+3cm=7cm
(2)解:MN= ![]() acm.理由如下:
acm.理由如下:
∵点M、N分别是AC、BC的中点,
∴MC= ![]() AC,NC=
AC,NC= ![]() BC,
BC,
∴MN=MC+NC= ![]() AC+
AC+ ![]() BC=
BC= ![]() AB=
AB= ![]() acm
acm
(3)解:如图,
![]()
∵点M、N分别是AC、BC的中点,
∴MC= ![]() AC,NC=
AC,NC= ![]() BC,
BC,
∴MN=MC﹣NC= ![]() AC﹣
AC﹣ ![]() BC=
BC= ![]() (AC﹣BC)=
(AC﹣BC)= ![]() bcm.
bcm.
【解析】(1)根据点M、N分别是AC、BC的中点,得到MC=![]() AC,NC=
AC,NC=![]() BC,求出MN=MC+NC;(2)由(1)可知,C为线段AB上任一点,都能满足MN=
BC,求出MN=MC+NC;(2)由(1)可知,C为线段AB上任一点,都能满足MN=![]() acm;(3)根据题意,得到MN=MC﹣NC=
acm;(3)根据题意,得到MN=MC﹣NC=![]() bcm.
bcm.
【考点精析】根据题目的已知条件,利用线段长短的计量的相关知识可以得到问题的答案,需要掌握度量法:即用一把刻度量出两条线段的长度再比较;叠合法:从“形”的角度比较,观察点的位置.


科目:初中数学 来源: 题型:
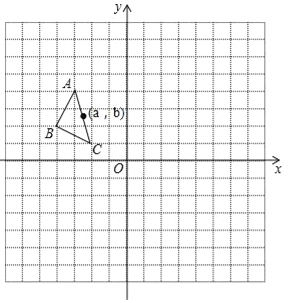
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标为A(﹣3,4),B(﹣4,2),C(﹣2,1),△ABC绕原点逆时针旋转90°,得到△A1B1C1,△A1B1C1向右平移6个单位,再向上平移2个单位得到△A2B2C2.
(1)画出△A1B1Cl和△A2B2C2;
(2)P(a,b)是△ABC的AC边上一点,△ABC经旋转、平移后点P的对应点分别为P1、P2,请写出点P1、P2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从2开始,连续的偶数相加,它们和的情况如下表:
(1)如果n =8时,那么S的值为;
(2)根据表中的规律猜想:用n的代数式表示S的公式为S=2+4+6+8+…+2n =;
(3)根据上题的规律计算102+104+106+…+2006的值(要有计算过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前节能灯在各城市已基本普及,今年某市面向县级及农村地区推广,为响应号召,朝阳灯饰商场用了4200元购进甲型和乙型两种节能灯.这两种型号节能灯的进价、售价如表:
进价(元/只) | 售价(元/只) | |
甲型 | 25 | 30 |
乙型 | 45 | 60 |
特别说明:毛利润=售价﹣进价
(1)朝阳灯饰商场销售甲型节能灯一只毛利润是元;
(2)朝阳灯饰商场购买甲,乙两种节能灯共100只,其中买了甲型节能灯多少只?
(3)现在朝阳灯饰商场购进甲型节能灯m只,销售完节能灯时所获的毛利润为1080元.求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了创设全新的校园文化氛围,进一步组织学生开展课外阅读,让学生在丰富多彩的书海中,扩大知识源,亲近母语,提高文学素养.某校准备开展“与经典为友、与名著为伴”的阅读活动,活动前对本校学生进行了“你最喜欢的图书类型(只写一项)”的随机抽样调查,相关数据统计如下:
请根据以上信息解答下列问题: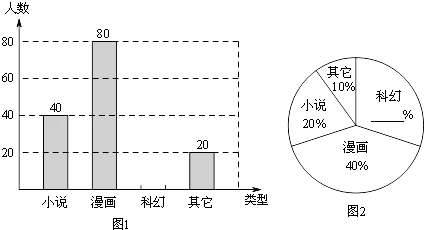
(1)该校对多少名学生进行了抽样调查?
(2)请将图1和图2补充完整;并求出扇形统计图中小说所对应的圆心角度数.
(3)已知该校共有学生800人,利用样本数据估计全校学生中最喜欢小说人数约为多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列条件不能判定四边形ABCD是平行四边形的是( )
A.AB∥CD,AD∥BC
B.AD=BC,AB=CD
C.AB∥CD,AD=BC
D.∠A=∠C,∠B=∠D
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com