
分析 (1)设二次函数的解析式为y=a(x-x1)(x-x2),把(-1,0),(3,0)代入得出y=a(x+1)(x-3),把(1,-5)代入求出a即可;
(2)设二次函数的解析式为y=a(x-h)2+k,代入顶点坐标,再代入(0,7)求出a即可;
(3)设二次函数的解析式为y=a(x-x1)(x-x2),代入点的坐标求出a即可.
解答 解:(1)设二次函数的解析式为y=a(x-x1)(x-x2),
把(-1,0),(3,0)代入得:y=a(x+1)(x-3),
把(1,-5)代入得:-5=a(1+1)(1-3),
解得:a=$\frac{5}{4}$,
所以二次函数的解析式为:y=$\frac{5}{4}$(x+1)(x-3),即y=$\frac{5}{4}$x2-$\frac{5}{2}$x-$\frac{15}{4}$;
(2)设二次函数的解析式为y=a(x-h)2+k,
∵当x=3时,y最小值=-1,
∴顶点坐标为(3,-1),
代入得:y=a(x-3)2-1,
把(0,7)代入得:a(0-3)2-1=7,
解得:a=$\frac{8}{9}$,
所以二次函数的解析式为:y=$\frac{8}{9}$(x-3)2-1,即y=$\frac{8}{9}$x2-$\frac{16}{3}$x+7;
(3)设二次函数的解析式为y=a(x-x1)(x-x2),
∵与x轴交点的横坐标分别是x1=-3,x2=1,
∴把(-3,0),(1,0)代入得:y=a(x+3)(x-1),
∵与y轴交点为(0,-2),
∴代入得:a(0+3)(0-1)=-2,
解得:a=$\frac{2}{3}$,
所以二次函数的解析式为:y=$\frac{2}{3}$(x+3)(x-1),即y=$\frac{2}{3}$x2+$\frac{4}{3}$x-2.
点评 本题考查了用待定系数法求二次函数的解析式的应用,能正确设解析式是解此题的关键,利用待定系数法求二次函数解析式时,注意合理利用抛物线解析式的三种形式.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | AB=CD,AD=BC | B. | AB∥CD,AB=CD | C. | AB=CD,AD∥BC | D. | AB∥CD,AD∥BC |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
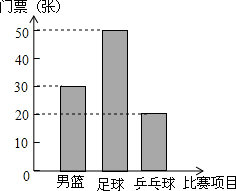 下表为抄录北京奥运会官方票务网公布的三种球类比赛的部分门票价格,某公司购买的门票种类、数量水质的统计图表如下:
下表为抄录北京奥运会官方票务网公布的三种球类比赛的部分门票价格,某公司购买的门票种类、数量水质的统计图表如下:| 比赛项目 | 票价(元/张) |
| 足球 | 1000 |
| 男篮 | 800 |
| 乒乓球 | x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com