Question

11．在一次羽毛球赛中，甲运动员在离地$\frac{36}{25}$米的P点处发球，球的运动轨迹PAN看作一个抛物线的一部分，当球运动到最高点A时，其高度为4米，离甲运动员站立地点O的水平距离为4米，球网BC离点O的水平距离为4.5米，以点O为原点建立如图所示的坐标系，乙运动员站立地点M的坐标为（m，0）．
（1）求抛物线的解析式（不要求写自变量的取值范围）；
（2）羽毛球边距离点C的水平距离为5.18米，此次发球是否会出界？
（3）乙原地起跳后可接球的最大高度为3米，若乙因为接球高度不够而失球，求m的取值范围．

Answer 1

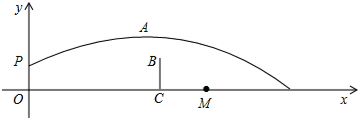
分析 （1）设抛物线解析式为y=a（x-4）²+4，将点（0，$\frac{36}{25}$）代入可得出a的值，继而得出抛物线解析式；
（2）令y=0，可得出ON的长度，由NC=ON-OC即可得出答案．
（3）先计算出刚好接到球时m的值，从而结合所给图形可得出运动员接球高度不够m的取值范围．

解答 解：（1）设抛物线解析式为y=a（x-4）²+4，将点（0，$\frac{36}{25}$）代入可得：$\frac{36}{25}$=a（0-4）²+4，
解得：a=-$\frac{4}{25}$．
故抛物线的解析式为：y=-$\frac{4}{25}$（x-4）²+4．
（2）当y=0时，-$\frac{4}{25}$（x-4）²+4=0，
解得：x₁=-1（舍去），x₂=9，
即ON=9，
∵OC=4.5，
∴CN=9-4.5=4.5＜5.18，
∴此次发球不会出界；
（3）若运动员乙原地起跳到最大高度时刚好接到球，
此时-$\frac{4}{25}$（m-4）²+4=3，
解得：m₁=1.5，m₂=6.5，
∴，1.5＜m＜6.5，
∵OC=4.5，乙运动员接球时不能触网，
∴m的取值范围为：4.5＜m＜6.5．

点评 本题考查了二次函数的应用，涉及了利用待定系数法求二次函数解析式的知识，解答本题的关键是建立直角坐标系，将实际问题转化为数学模型．