
分析 (1)先因式分解,根据非负数的性质“两个非负数相加,和为0,这两个非负数的值都为0”求得答案即可;
(2)先整体代入(1)中的数值,再进一步把a2-3a=-1变形求得a+$\frac{1}{a}$代入得出答案即可,
解答 解:(1)∵$\sqrt{{a}^{2}-3a+1}$+b2+2b+1=$\sqrt{{a}^{2}-3a+1}$+(b+1)2=0.
∴a2-3a=-1,b=-1,
(2)把a2-3a=-1,b=-1代入得
原式=3(a2-3a)+3a+$\frac{1}{a^2}$-b2=3a+$\frac{1}{a^2}$-4,
∵a2-3a=-1,
∴a2=3a-1,a+$\frac{1}{a}$=3,
∴原式=3a+$\frac{1}{a^2}$-4=a2+$\frac{1}{a^2}$-3=(a+$\frac{1}{a}$)2-2-3=4.
点评 此题考查了配方法的应用,以及非负数的性质,熟练掌握完全平方公式,以及恒等变形是解本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
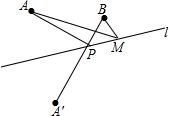 如图,已知A,B两点在直线1的同侧,点A′与A关于直线l对称,连接A′B交l于点P.若A′B=a.
如图,已知A,B两点在直线1的同侧,点A′与A关于直线l对称,连接A′B交l于点P.若A′B=a.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
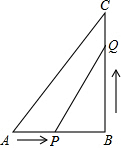 如图所示,△ABC中,AB=6cm,BC=8cm,∠B=90°,点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果p、Q分别从A、B同时出发,移动了t秒:
如图所示,△ABC中,AB=6cm,BC=8cm,∠B=90°,点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果p、Q分别从A、B同时出发,移动了t秒:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
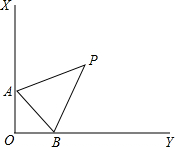 如图所示,∠XOY=90°,点A,B分别为射线OX,OY上两点,∠XAB和∠YBA的角平分线交于点P,则当A,B移动时,∠P的大小是否发生变化?如果保持不变,请说明理由;如果随A,B的移动而变化,请求出变化范围.
如图所示,∠XOY=90°,点A,B分别为射线OX,OY上两点,∠XAB和∠YBA的角平分线交于点P,则当A,B移动时,∠P的大小是否发生变化?如果保持不变,请说明理由;如果随A,B的移动而变化,请求出变化范围.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
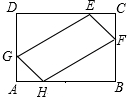 如图,在矩形ABCD中,AB=8,BC=4,点H、F、E、G分别在AB、BC、CD、DA上,且AH=AG=CE=CF=x,四边形EFHG的面积为y.
如图,在矩形ABCD中,AB=8,BC=4,点H、F、E、G分别在AB、BC、CD、DA上,且AH=AG=CE=CF=x,四边形EFHG的面积为y.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com