
【题目】如图,在四边形ABCD中,对角线AC,BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°.

(1)求证:四边形ABCD是矩形;
(2)若∠ADF:∠FDC=3:2,DF⊥AC,求∠BDF的度数.
【答案】(1)见解析;(2)∠BDF=18°.
【解析】
(1)先证明四边形ABCD是平行四边形,求出∠ABC=90°,然后根据矩形的判定定理,即可得到结论;
(2)求出∠FDC的度数,根据三角形的内角和,求出∠DCO,然后得到OD=OC,得到∠CDO,即可求出∠BDF的度数.
(1)证明:∵AO=CO,BO=DO,
∴四边形ABCD是平行四边形,
∴∠ABC=∠ADC,
∵∠ABC+∠ADC=180°,
∴∠ABC=∠ADC=90°,
∴四边形ABCD是矩形;
(2)解:∵∠ADC=90°,∠ADF:∠FDC=3:2,
∴∠FDC=36°,
∵DF⊥AC,
∴∠DCO=90°﹣36°=54°,
∵四边形ABCD是矩形,
∴CO=OD,
∴∠ODC=∠DCO=54°,
∴∠BDF=∠ODC﹣∠FDC=18°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
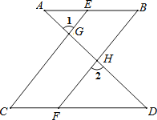
【题目】完成下面推理过程:
如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
∵∠1=∠2(已知),
且∠1=∠CGD( ),
∴∠2=∠CGD( ).
∴CE∥BF( ).
∴∠ =∠C( ).
又∵∠B=∠C(已知),
∴∠ =∠B(等量代换).
∴AB∥CD( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC=BC,∠ACB=90°,AE平分∠BAC,BF⊥AE,交AC延长线于F,且垂足为E,则下列结论:①AD=BF;②∠BAE=∠FBC;③S△ADB=S△ADC;④AC+CD=AB;⑤AD=2BE.其中正确的结论有______(填写序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索题:(x-1)((x+1)=x2-1,
(x-1)(x2+x+1)=x3-1,
(x-1)(x3+x2+x+1)=x4-1,
(x-1)(x4+x3+x2+x+1)=x5-1.
(1)观察以上各式并猜想:
①(x-1)(x6+x5+x4+x3+x2+x+1)=________________________;
②(x-1)(xn+xn-1+xn-2+…+x3+x2+x+1)= ________________________;
(2)请利用上面的结论计算:
①(-2)50+(-2)49+(-2)48+…+(-2)+1
②若x1007+x1006+…+x3+x2+x+1=0,求x2016的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】分已知关于x的一元二次方程(m-2)x2+(2m+1)x+m=0有两个实数根x1,x2.
(1)求m的取值范围.
(2)若|x1|=|x2|,求m的值及方程的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1+∠2=180o, ∠3=∠B,试说明∠DEC+∠C=180o.请完成下列填空:

解:∵∠1+∠2=180o(已知)
又∵∠1+∠4=180o(平角定义)
∴∠2=∠4(________)
∴______∥______(_________)
∴∠3 = ∠ADE(__________)
又∵∠3=∠B(已知)
∴∠ADE=∠B(等量代换)
∴BC∥_____(_________)
∴∠DEC+∠C=180o(__________)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AE⊥BC,AF⊥CD,垂足分别为E,F,且BE=DF.
(1)求证:ABCD是菱形;
(2)若AB=5,AC=6,求ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直角三角形的铁片ABC的两条直角边BC,AC的长分别为3cm和4cm,如图所示分别采用⑴,⑵两种方法,剪去一块正方形铁片,为了使剪去正方形铁片后剩下的边角料较少,试比较哪一种剪法较为合理,并说明理由.
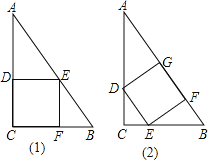
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com