
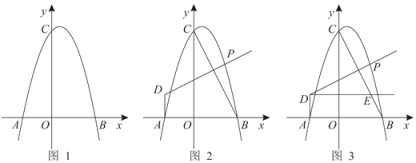
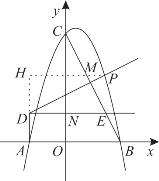
【题目】已知:如图,抛物线![]() 交x轴于A(-2,0),B(3,0)两点,交y轴于点C(0,6).
交x轴于A(-2,0),B(3,0)两点,交y轴于点C(0,6).
(1)写出a,b,c的值;
(2)连接BC,点P为第一象限抛物线上一点,过点A作AD⊥x轴,过点P作PD⊥BC于交直线AD于点D,设点P的横坐标为t,AD长为h.
①求h与t的函数关系式和h的最大值(请求出自变量t的取值范围);
②过第二象限点D作DE∥AB交BC于点E,若DP=CE,时,求点P的坐标.
【答案】(1)a=-1,b=1,c=6;(2)① ,当
,当![]() 时,h有最大值为
时,h有最大值为![]() ,当
,当![]() <t<3时,
<t<3时,![]() 无最大值,②符合条件的点P的坐标为(2,4).
无最大值,②符合条件的点P的坐标为(2,4).
【解析】
(1)根据待定系数法求解;(2)①如图,过点P作PG⊥x于点G,过点D作DK∥x轴交PG于点K,根据三角函数值和矩形性质得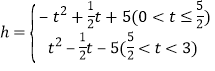 ,再求最值;②如图,过点P作PH⊥AD交AD的延长线于点H,根据全等三角形判定和性质,△PHD≌△CNE(AAS),PH=CN=OC-ON,根据矩形性质,t+2=
,再求最值;②如图,过点P作PH⊥AD交AD的延长线于点H,根据全等三角形判定和性质,△PHD≌△CNE(AAS),PH=CN=OC-ON,根据矩形性质,t+2=![]() ,解得
,解得![]() ,
,![]() (舍去),把t=2代入抛物线
(舍去),把t=2代入抛物线![]() ,可求点P(2,4).当点D在第三象限时,不存在点P满足DP=CE.故符合条件的点P的坐标为(2,4).
,可求点P(2,4).当点D在第三象限时,不存在点P满足DP=CE.故符合条件的点P的坐标为(2,4).
(1)根据题意得
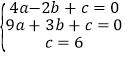
所以,a=-1,b=1,c=6;
(2)①如图,过点P作PG⊥x于点G,过点D作DK∥x轴交PG于点K,
∵PD⊥BC,DK⊥y轴,∠BCO=∠PDK,OB=3,OC=6,
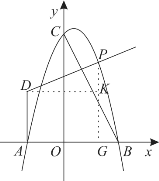
∴tan∠BCO=tan∠PDK=![]() ,DK=t+2,PK=
,DK=t+2,PK=![]() DK=
DK=![]() ,
,
∵DK∥AB,AD⊥AB,∴四边形ADKG为矩形,
∴AD=KG,
h=AD=KG=|PG-PK|=![]()
令![]() ,
,![]() ,
,![]() ,
,![]() (不合题意,舍去)
(不合题意,舍去)
∴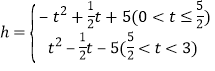
当0<t≤![]() 时,
时,![]()
![]()
∴当![]() 时,h有最大值为
时,h有最大值为![]()
当![]() <t<3时,
<t<3时,![]() 无最大值.
无最大值.
②如图,过点P作PH⊥AD交AD的延长线于点H,
∵PD⊥BC,∴∠PHD=∠ECE=90°-∠CMH
在△PHD与△CNE中,
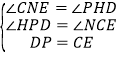 ,
,
∴△PHD≌△CNE(AAS),
∴PH=CN=OC-ON,
∵四边形ADNO为矩形,
∴CN=![]() =
=![]() ,PH=t+2,
,PH=t+2,
∴t+2=![]() ,
,
解得![]() ,
,![]() (舍去),
(舍去),
把t=2代入抛物线![]() ,∴点P(2,4).
,∴点P(2,4).
当点D在第三象限时,不存在点P满足DP=CE.
∴符合条件的点P的坐标为(2,4).


科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+x+6及一次函数y=﹣x+m,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新函数(如图所示),请你在图中画出这个新图象,当直线y=﹣x+m与新图象有4个交点时,m的取值范围是( )

A. ﹣![]() <m<3 B. ﹣
<m<3 B. ﹣![]() <m<2 C. ﹣2<m<3 D. ﹣6<m<﹣2
<m<2 C. ﹣2<m<3 D. ﹣6<m<﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CA=CB,∠C=90°,点D是BC的中点,将△ABC沿着直线EF折叠,使点A与点D重合,折痕交AB于点E,交AC于点F,那么sin∠BED的值为( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知E,F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M,O为BD的中点,则下列结论:
①∠AME=90°;②∠BAF=∠EDB;③∠BMO=90°;④MD=2AM=4EM;⑤AM=![]() MF.其中正确结论的是( )
MF.其中正确结论的是( )

A. ①③④ B. ②④⑤ C. ①③④⑤ D. ①③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表显示了同学们用计算机模拟随机投针实验的某次实验的结果.
投针次数n | 1000 | 2000 | 3000 | 4000 | 5000 | 10000 | 20000 |
针与直线相交的次数m | 454 | 970 | 1430 | 1912 | 2386 | 4769 | 9548 |
针与直线相交的频率p=
| 0.454 | 0.485 | 0.4767 | 0.478 | 0.4772 | 0.4769 | 0.4774 |
下面有三个推断:
①投掷1000次时,针与直线相交的次数是454,针与直线相交的概率是0.454;
②随着实验次数的增加,针与直线相交的频率总在0.477附近,显示出一定的稳定性,可以估计针与直线相交的概率是0.477;
③若再次用计算机模拟此实验,则当投掷次数为10000时,针与直线相交的频率一定是0.4769.
其中合理的推断的序号是:_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
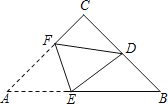
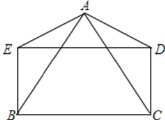
【题目】如图,AB=AC,AD=AE,DE=BC,且∠BAD=∠CAE.
(1)求证:△ABE≌△ACD;
(2)判断四边形BCDE的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
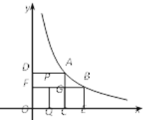
【题目】我们知道,如果一个矩形的宽与长之比为![]() ,那么这个矩形就称为黄金矩形.如图,已知A、B两点都在反比例函数y=
,那么这个矩形就称为黄金矩形.如图,已知A、B两点都在反比例函数y=![]() (k>0)位于第一象限内的图像上,过A、B两点分别作坐标轴的垂线,垂足分别为C、D和E、F,设AC与BF交于点G,已知四边形OCAD和CEBG都是正方形.设FG、OC的中点分别为P、Q,连接PQ.给出以下结论:①四边形ADFG为黄金矩形;②四边形OCGF为黄金矩形;③四边形OQPF为黄金矩形.以上结论中,正确的是( )
(k>0)位于第一象限内的图像上,过A、B两点分别作坐标轴的垂线,垂足分别为C、D和E、F,设AC与BF交于点G,已知四边形OCAD和CEBG都是正方形.设FG、OC的中点分别为P、Q,连接PQ.给出以下结论:①四边形ADFG为黄金矩形;②四边形OCGF为黄金矩形;③四边形OQPF为黄金矩形.以上结论中,正确的是( )
A. ①B. ②C. ②③D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
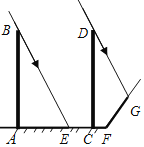
【题目】如图,高度相同的两根电线杆AB、CD均垂直于地面AF,某时刻电线杆AB的影子为地面上的线段AE,电线杆CD的影子为地面上的线段CF和坡面上的线段FG.已知坡面FG的坡比i=1:0.75,又AE=6米,CF=1米,FG=5米,那么电线杆AB的高度为______米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com