
【题目】(1)如图,在△ABC中,∠A是锐角,点D,E分别在AB,AC上,且∠DCB=∠EBC=![]() ∠A,BE与CD相交于点O,探究BD与CE之间的数量关系,并证明你的结论.
∠A,BE与CD相交于点O,探究BD与CE之间的数量关系,并证明你的结论.
(2)已知四边形ABCD,连接AC、BD交于O,且满足条件:AB+CD=AD+BC,AB2+AD2=BC2+DC2,请探究AC与BD的关系,并说明理由.
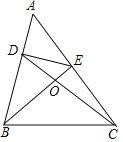
【答案】(1)BD=CE,理由见解析;(2)AC与BD的关系是:BD垂直平分AC;理由见解析.
【解析】
(1)以C为顶点作∠FCB=∠DBC,CF交BE于F点,证明△BDC≌△CFB(ASA),得出BD=CF,∠BDC=∠CFB,再证出∠CFB=∠CEF,得出CE=CF,即可得出结论;
(2)由AB+DC=AD+BC,AB2+AD2=BC2+DC2,可证得AB=BC,DC=AD,即可得出BD垂直平分AC.
解:(1)BD=CE,
证明:以C为顶点作∠FCB=∠DBC,CF交BE于F点,如图1所示:
在△BDC和△CFB中, ,
,
∴△BDC≌△CFB(ASA),
∴BD=CF,∠BDC=∠CFB,
∵∠DCB=∠EBC=![]() ∠A,
∠A,
∴∠DCB+∠EBC=∠A,
∵∠DCB+∠EBC=∠FOC,
∴∠FOC=∠A,
∵∠BDC=∠A+∠ACD,
∴∠CFB=∠A+∠ACD,
∴∠CFB=∠FOC+∠ACD,
∵∠FEC=∠FOC+∠ACD,
∴∠CFB=∠CEF,
∴CE=CF,
∴BD=CE;
(2)AC与BD的关系是:BD垂直平分AC;
理由:如图2所示:
∵AB2+AD2=BC2+DC2,
∴AB2﹣DC2=BC2﹣AD2,
∴(AB+DC)(AB﹣DC)=(AD+BC)(BC﹣AD),
∵AB+DC=AD+BC,
∴AB﹣DC=BC﹣AD,
∴AB=BC,DC=AD,
∴点B在AC的垂直平分线上,点D在AC的垂直平分线上,
∴BD垂直平分AC.




科目:初中数学 来源: 题型:
【题目】如图,BF和CE分别是钝角△ABC(∠ABC是钝角)中AC、AB边上的中线,又BF⊥CE,垂足是G,过点G作GH⊥BC,垂足为H.
(1)求证:GH2=BHCH;
(2)若BC=20,并且点G到BC的距离是6,则AB的长为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
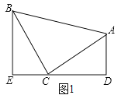
【题目】(1)(模型建立)如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED与D,过B作BE⊥ED于E,求证:△BEC≌△CDA;
(2)(模型应用):已知直线![]() 与y轴交于A点,与x轴交于B点,将线段AB绕点B逆时针旋转90度,得到线段BC,过点A,C作直线,求直线AC的解析式;
与y轴交于A点,与x轴交于B点,将线段AB绕点B逆时针旋转90度,得到线段BC,过点A,C作直线,求直线AC的解析式;

查看答案和解析>>
科目:初中数学 来源: 题型:
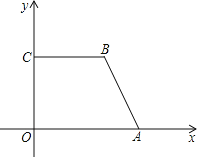
【题目】如图,点A在x轴上,BC⊥y轴于C,点B的横坐标为a,AB=2a,∠B=120°,在y轴上找一点P,使PA+PB最小,请画出点P,并求PA+PB的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】折叠圆心为![]() 、半径为
、半径为![]() 的圆形纸片,使圆周上的某一点
的圆形纸片,使圆周上的某一点![]() 与圆心
与圆心![]() 重合.对圆周上的每一点,都这样折叠纸片,从而都有一条折痕.那么,所有折痕所在直线上点的全体为( )
重合.对圆周上的每一点,都这样折叠纸片,从而都有一条折痕.那么,所有折痕所在直线上点的全体为( )
A. 以![]() 为圆心、半径为
为圆心、半径为![]() 的圆周 B. 以
的圆周 B. 以![]() 为圆心、半径为
为圆心、半径为![]() 的圆周
的圆周
C. 以![]() 为圆心、半径为
为圆心、半径为![]() 的圆内部分 D. 以
的圆内部分 D. 以![]() 为圆心、半径为
为圆心、半径为![]() 的圆周及圆外部分
的圆周及圆外部分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y=![]() (k<0)的图象与矩形ABCD的边相交于E、F两点,且BE=2AE,E(﹣1,2).
(k<0)的图象与矩形ABCD的边相交于E、F两点,且BE=2AE,E(﹣1,2).

(1)求反比例函数的解析式;
(2)连接EF,求△BEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《孙子算经》是中国传统数学最重要的著作,约成书于四、五世纪.现在传本的《孙子算经》共三卷.卷上叙述算筹记数的纵横相间制度和筹算乘除法则;卷中举例说明筹算分数算法和筹算开平方法;卷下记录算题,不但提供了答案,而且还给出了解法.其中记载:“今有木,不知长短.引绳度之,余绳四尺五,屈绳量之,不足一尺.问木长几何?”
译文:“用一根绳子去量一根长木,绳子还剩余4.5尺,将绳子对折再量长木,长木还剩余1尺,问长木长多少尺?”
请解答上述问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,H是△ABC的高AD,BE的交点,且DH=DC,则下列结论:①BD=AD;②BC=AC;③BH=AC;④CE=CD中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com