
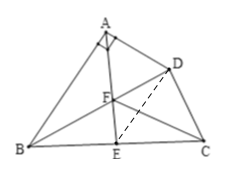
【题目】如图,在四边形![]() 中,
中,![]() 平分
平分![]() ,
,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 与
与![]() 相交于点
相交于点![]() .若
.若![]() ,
,![]() ,则
,则![]() 的长为_____.
的长为_____.

【答案】![]()
【解析】
连接DE,在Rt△CBD和Rt△ABD中,利用30度角的余弦求出BD和AB的长,利用直角三角形中线的性质可求出DE=BE=3,即:∠BDE=∠ABD,进而判断出DE∥AB,即可得出△DEF∽△BAF,根据相似三角形的性质即可得答案.
∵BC=6,∠CBD=30°,
∴BD=BC![]() cos30°=3
cos30°=3![]() ,
,
∵BD平分∠ABC,∠CBD=30°,
∴∠ABD=30°,
∵∠BAD=90°,
∴AB=BD![]() cos30°=
cos30°=![]() ,
,
∵E是BC的中点,∠BDC=90°,
∴DE=BE=![]() BC=3,
BC=3,
∴∠BDE=∠DBE,
∴BDE=∠ABD,
∴DE//AB,
∴△DEF∽△BAF,
∴![]() ,即
,即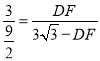
解得:DF=![]() .
.
故答案为:![]()


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
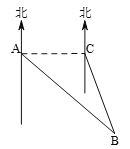
【题目】如图,小岛![]() 正好在深水港口
正好在深水港口![]() 的东南方向,一艘集装箱货船从港口
的东南方向,一艘集装箱货船从港口![]() 出发,沿正东方向以每小时30千米的速度行驶,40分钟后在
出发,沿正东方向以每小时30千米的速度行驶,40分钟后在![]() 处测得小岛
处测得小岛![]() 在它的南偏东
在它的南偏东![]() 方向,求小岛
方向,求小岛![]() 离深水港口
离深水港口![]() 的距离(精确到0.1千米).参考数据:
的距离(精确到0.1千米).参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() x2﹣x+4与x轴交于A,B两点(A在B的左侧),与y轴交于点C.
x2﹣x+4与x轴交于A,B两点(A在B的左侧),与y轴交于点C.
(1)求点A,点B的坐标;
(2)P为第二象限抛物线上的一个动点,求△ACP面积的最大值.
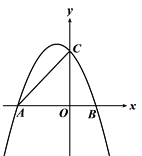
查看答案和解析>>
科目:初中数学 来源: 题型:
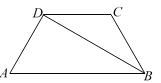
【题目】已知:如图,在梯形ABCD中,DC∥AB,AD=BC,BD平分∠ABC,∠A=60°.
求:(1)求∠CDB的度数;
(2)当AD=2时,求对角线BD的长和梯形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于![]() 的一元二次方程
的一元二次方程![]() 与
与![]() ,下列判断不正确的是( )
,下列判断不正确的是( )
A.若方程![]() 有两个实数根,则方程
有两个实数根,则方程![]() 也有两个实数根;
也有两个实数根;
B.如果![]() 是方程
是方程![]() 的一个根,那么
的一个根,那么![]() 是
是![]() 的一个根;
的一个根;
C.如果方程![]() 与
与![]() 有一个根相等,那么这个根是1;
有一个根相等,那么这个根是1;
D.如果方程![]() 与
与![]() 有一个根相等,那么这个根是1或-1.
有一个根相等,那么这个根是1或-1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一堂数学实践课上,赵老师给出了下列问题:
提出问题
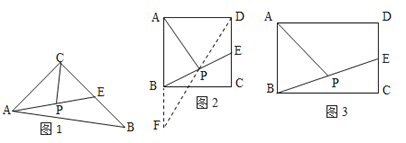
(1)如图1,在△ABC中,E是BC的中点,P是AE的中点,就称CP是△ABC的“双中线”,∠ACB=900,AC=3,AB=5.则CP=___;
探究规律
(2)在图2中,E是正方形ABCD一边上的中点,P是BE上的中点,则称AP是正方形ABCD的“双中线”,若AB=4.则AP的长为_____;
(3)在图3中,AP是矩形ABCD的“双中线”, 若AB=4,BC=6,请仿照(2)中的方法求出AP的长,并说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
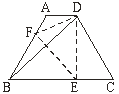
【题目】如图,等腰梯形ABCD中,AD∥BC,∠DBC=45°,翻折梯形ABCD,使点B重合于点D,折痕分别交边AB、BC于点F、E,若AD=2,BC=8.则(1)BE的长为_________. (2)∠CDE的正切值为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com