
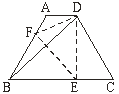
【题目】如图,等腰梯形ABCD中,AD∥BC,∠DBC=45°,翻折梯形ABCD,使点B重合于点D,折痕分别交边AB、BC于点F、E,若AD=2,BC=8.则(1)BE的长为_________. (2)∠CDE的正切值为________.
【答案】BE=5; tan∠CDE=![]()
【解析】
(1)由轴对称的性质可以得出△BFE≌△DFE,从而得出DE=BE,由∠DBC=45°可以得出∠BED=90°,过A作AG⊥BC于G,可以求出BG=3,可以求出BE的值.
(2)根据tan∠CDE=![]() ,由(1)的结论可以求出其值.
,由(1)的结论可以求出其值.
(1)由题意得△BFE≌△DFE,
∴DE=BE.
又∵在△BDE中,∠DBE=45°,
∴∠BDE=∠DBE=45°,
∴∠BED=90°,即DE⊥BC.
∵在等腰梯形ABCD中,AD=2,BC=8,
过A作AG⊥BC于G,

∵四边形AGED是矩形.
∴AD=GE=2,AG=DE.
∵四边形ABCD是等腰梯形,
∴AB=CD,
∵∠AGB=∠DEC=90°
Rt△ABG和Rt△DCE中,
![]()
∴Rt△ABG≌Rt△DCE(HL),
∴BG=EC=3.
∴BE=5
(2)由(1)得DE=BE=5,
在△DEC中,∠DEC=90°,DE=5,EC=3,
∴tan∠CDE=![]() =
=![]()
![]()
故答案为:(1) BE=5; (2) tan∠CDE=![]()


科目:初中数学 来源: 题型:
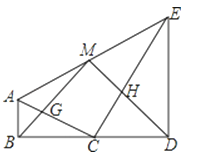
【题目】已知:如图,Rt△CDE中,∠ABC=∠CDE=90°,且BC与CD共线,联结AE,点M为AE中点,联结BM,交AC于点G,联结MD,交CE于点H
(1)求证:MB=MD;
(2)当AB=BC,DC=DE时,求证:四边形MGCH为矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
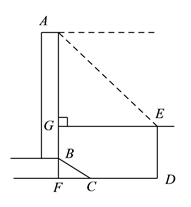
【题目】如图所示,某办公大楼正前方有一根高度是![]() 米的旗杆
米的旗杆![]() ,从办公楼顶端
,从办公楼顶端![]() 测得旗杆顶端
测得旗杆顶端![]() 的俯角
的俯角![]() 是
是![]() ,旗杆底端
,旗杆底端![]() 到大楼前梯坎底边的距离
到大楼前梯坎底边的距离![]() 是
是![]() 米,梯坎坡长
米,梯坎坡长![]() 是
是![]() 米,梯坎坡度
米,梯坎坡度![]() ,求大楼
,求大楼![]() 的高度.(精确到
的高度.(精确到![]() 米,参与数据:
米,参与数据: ![]() ,
, ![]() ,
, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习反比例函数的图象时,他的老师要求同学们根据“探索一次函数y1=x+1的图象”的基本步骤,在纸上逐步探索函数y2=![]() 的图象,并且在黑板上写出4个点的坐标:A(
的图象,并且在黑板上写出4个点的坐标:A(![]() ,
,![]() ),B(1,2),C(1,
),B(1,2),C(1,![]() ),D(﹣2,﹣1).
),D(﹣2,﹣1).
(1)在A、B、C、D四个点中,任取一个点,这个点既在直线y1=x+1又在双曲线y2=![]() 上的概率是多少?
上的概率是多少?
(2)小明从A、B、C、D四个点中任取两个点进行描点,求两点都落在双曲线y2=![]() 上的概率.
上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
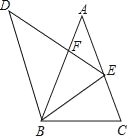
【题目】如图,在△ABC中,∠A=36°,AC=AB=2,将△ABC绕点B逆时针方向旋转得到△DBE,使点E在边AC上,DE交AB于点F,则△AFE与△DBF的面积之比等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)关于x,y的方程组![]() 满足x+y=5,求m的值.
满足x+y=5,求m的值.
(2)关于x的一元二次方程x2﹣(m﹣1)x﹣m=0的两个根x1,x2满足x12+x22=5,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某篮球队运动员进行3分球投篮成绩测试,每人每天投3分球10次,对甲、乙两名队员在5天中进球的个数统计如果如下:队员每人每天进球数(个)经过计算,甲进球的平均数为x甲=8和方差S2甲=3.2.

(1)求乙进球的平均数x乙和方差S2乙;
(2)现在需要根据以上数据,从甲、乙二人中选出一人去参加3分球投篮大赛,你认为应该选哪名队员?说说你的理由?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市开展“美丽家乡,创卫同行”活动,某校倡议学生利用双休日参加义务劳动,为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制了不完整的统计图①和图②,请根据相关信息,解答下列问题:
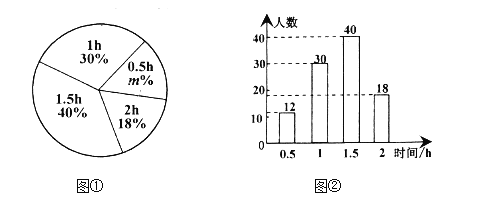
(Ⅰ)本次接受随机抽样调查的学生人数为 ,图①中![]() 的值是 ;
的值是 ;
(Ⅱ)求本次调查获取的样本数据的平均数、众数和中位数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com