
【题目】某篮球队运动员进行3分球投篮成绩测试,每人每天投3分球10次,对甲、乙两名队员在5天中进球的个数统计如果如下:队员每人每天进球数(个)经过计算,甲进球的平均数为x甲=8和方差S2甲=3.2.

(1)求乙进球的平均数x乙和方差S2乙;
(2)现在需要根据以上数据,从甲、乙二人中选出一人去参加3分球投篮大赛,你认为应该选哪名队员?说说你的理由?
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:
【题目】在一堂数学实践课上,赵老师给出了下列问题:
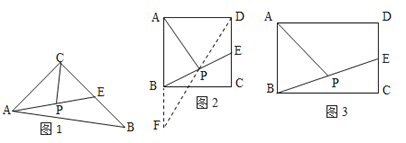
提出问题
(1)如图1,在△ABC中,E是BC的中点,P是AE的中点,就称CP是△ABC的“双中线”,∠ACB=900,AC=3,AB=5.则CP=___;
探究规律
(2)在图2中,E是正方形ABCD一边上的中点,P是BE上的中点,则称AP是正方形ABCD的“双中线”,若AB=4.则AP的长为_____;
(3)在图3中,AP是矩形ABCD的“双中线”, 若AB=4,BC=6,请仿照(2)中的方法求出AP的长,并说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰梯形ABCD中,AD∥BC,∠DBC=45°,翻折梯形ABCD,使点B重合于点D,折痕分别交边AB、BC于点F、E,若AD=2,BC=8.则(1)BE的长为_________. (2)∠CDE的正切值为________.
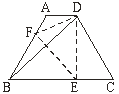
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知Rt△ABC,∠ABC=90°,顶点A在第一象限,B,C在x轴的正半轴上(C在B的右侧),BC=2,AB=2![]() ,将△ABC沿AC翻折得△ADC,点A和点D都在反比例函数y=
,将△ABC沿AC翻折得△ADC,点A和点D都在反比例函数y=![]() 的图象上,则k的值是_____.
的图象上,则k的值是_____.
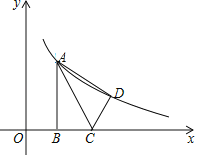
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=90°,AB=2cm,AC=4cm.动点P从点A出发,沿AB方向以1cm/s的速度向点B运动,动点Q从点B同时出发,沿BA方向以1cm/s的速度向点A运动.当点P到达点B时,P,Q两点同时停止运动,以AP为一边向上作正方形APDE,过点Q作QF∥BC,交AC于点F.设点P的运动时间为ts,正方形和梯形重合部分的面积为Scm2.
(1)当t= _________ s时,点P与点Q重合;
(2)当t= _________ s时,点D在QF上;
(3)当点P在Q,B两点之间(不包括Q,B两点)时,求S与t之间的函数关系式.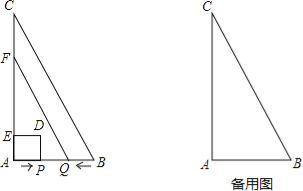
查看答案和解析>>
科目:初中数学 来源: 题型:
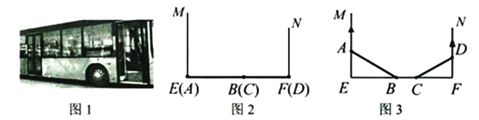
【题目】图2、图3是某公共汽车双开门的俯视示意图,ME,EF,FN是门轴的滑动轨道,![]() ,两门AB,CD的门轴A,B,C,D都在滑动轨道上,两门关闭时图2,A,D分别在E,F处,门缝忽略不计(即B,C重合);两门同时开启,A,D分别沿
,两门AB,CD的门轴A,B,C,D都在滑动轨道上,两门关闭时图2,A,D分别在E,F处,门缝忽略不计(即B,C重合);两门同时开启,A,D分别沿![]() ,
,![]() 的方向匀速滑动,带动B,C滑动;B到达E时,C恰好到达F,此时两门完全开启.已知
的方向匀速滑动,带动B,C滑动;B到达E时,C恰好到达F,此时两门完全开启.已知![]() .(1)如图3,当
.(1)如图3,当![]() 时,
时,![]() ______cm.(2)在(1)的基础上,当A向M方向继续滑动15cm时,四边形ABCD的面积为______
______cm.(2)在(1)的基础上,当A向M方向继续滑动15cm时,四边形ABCD的面积为______![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为A(0,a),B(b,a),且a,b满足(a﹣3)2+|b﹣6|=0,现同时将点A,B分别向下平移3个单位,再向左平移2个单位,分别得到点A,B的对应点C,D,连接AC,BD,AB.

(1)求点C,D的坐标及四边形ABDC的面积S四边形ABCD;
(2)在y轴上是否存在一点M,连接MC,MD,使S△MCD=![]() S四边形ABCD?若存在这样一点,求出点M的坐标,若不存在,试说明理由;
S四边形ABCD?若存在这样一点,求出点M的坐标,若不存在,试说明理由;
(3)点P是直线BD上的一个动点,连接PA,PO,当点P在BD上移动时(不与B,D重合),直接写出∠BAP,∠DOP,∠APO之间满足的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
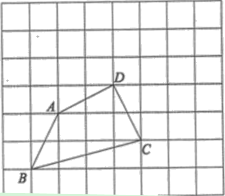
【题目】如图,在由边长都为1的小正方形组成的网格中,点![]() 均为格点.
均为格点.
(Ⅰ)线段![]() 的长度等于______;
的长度等于______;
(Ⅱ)若![]() 为线段
为线段![]() 上一点,且满足
上一点,且满足![]() ,请你借助无刻度直尺在给定的网格中面出满足条件的线段
,请你借助无刻度直尺在给定的网格中面出满足条件的线段![]() ,并简要说明你是怎么画出点
,并简要说明你是怎么画出点![]() ______________________.
______________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形的边长为1的网格中,点![]() 都在格点上。
都在格点上。

(Ⅰ)AC的长是_____________;
(Ⅱ)将四边形![]() 折叠,使点C与点4重合,折痕EF交BC于点E,交AD于点F,点D的对应点为Q,得五边形
折叠,使点C与点4重合,折痕EF交BC于点E,交AD于点F,点D的对应点为Q,得五边形![]() .请用无刻度的直尺在网格中画出折叠后的五边形,并简要说明点
.请用无刻度的直尺在网格中画出折叠后的五边形,并简要说明点![]() 的位置是如何找到的____________________.
的位置是如何找到的____________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com