
【题目】在一堂数学实践课上,赵老师给出了下列问题:
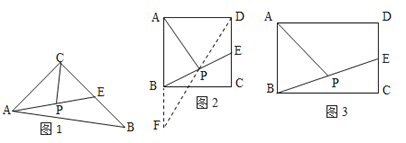
提出问题
(1)如图1,在△ABC中,E是BC的中点,P是AE的中点,就称CP是△ABC的“双中线”,∠ACB=900,AC=3,AB=5.则CP=___;
探究规律
(2)在图2中,E是正方形ABCD一边上的中点,P是BE上的中点,则称AP是正方形ABCD的“双中线”,若AB=4.则AP的长为_____;
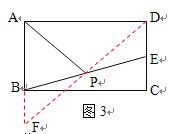
(3)在图3中,AP是矩形ABCD的“双中线”, 若AB=4,BC=6,请仿照(2)中的方法求出AP的长,并说明理由;
【答案】(1)![]() ;(2)
;(2)![]() ;(3)AP=3
;(3)AP=3![]()
【解析】
(1)先根据勾股定理求出BC=4,再根据双中线的定义得到E是BC的中点,故EC=2,利用勾股定理求出AE=![]() ,再根据直角三角形斜边上的中线求出CP的长;
,再根据直角三角形斜边上的中线求出CP的长;
(2)根据图中辅助线可证明△DEP≌△FBP,得到DE=BF,利用勾股定理求出DF的长,即可求出AP的长;
(3)连接DP并延长交AB的延长线于F ,证明△BPF≌△EPD,在Rt△ADF中,求出DF,在Rt△ADF中,求出AP.
解:(1)在Rt△ABC中,BC=![]() ,
,
∵CP是△ABC的“双中线”,
∴E是BC的中点,故EC=2,
在Rt△ACE中,AE=![]()
又P是AE中点,
所以CP=![]() AE=
AE=![]() ;
;
(2)如图2,连接DP,交AB延长线与F,∵CD∥AB,∴∠F=∠PDE, ∠PBF=∠PED,
又P是BE中点,∴BP=EP,∴△DEP≌△FBP
∴DE=BF
故AF=4+2=6,
在Rt△ADF中,DF=![]()
又P为DF中点,∴AP=![]() DF=
DF=![]()
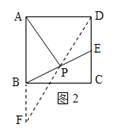
∴AP的长为![]() ;
;
(3)连接DP并延长交AB的延长线于F
∵矩形ABCD
∴AB∥CD
∴∠PBF=∠PED,∠F=∠PDE
∵P是BE的中点
∴PB=PE
∴△BPF≌△EPD
∴BF=DE=![]() CD=2
CD=2
在Rt△ADF中
DF=![]()
=![]()
=6![]()
在Rt△ADF中
AP=![]() DF=3
DF=3![]()


科目:初中数学 来源: 题型:
【题目】某商场计划购进A,B两种型号的手机,已知每部A型号手机的进价比每部B型号手机进价多500元,每部A型号手机的售价是2500元,每部B型号手机的售价是2100元.
(1)若商场用50000元共购进A型号手机10部,B型号手机20部,求A、B两种型号的手机每部进价各是多少元?
(2)为了满足市场需求,商场决定用不超过7.5万元采购A、B两种型号的手机共40部,且A型号手机的数量不少于B型号手机数量的2倍.
①该商场有哪几种进货方式?
②该商场选择哪种进货方式,获得的利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
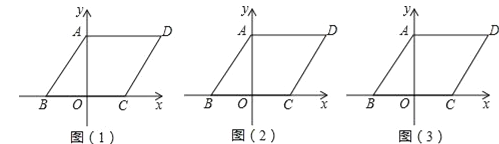
【题目】如图,在平面直角坐标系中,四边形ABCD是平行四边形,AD=6,若OA、OB的长是关于x的一元二次方程x2﹣7x+12=0的两个根,且OA>OB.
(1)求A、B的坐标.
(2)求证:射线AO是∠BAC的平分线.
(3)若点M在平面直角坐标系内,则在直线AB上是否存在点F,使以A、C、F、M为顶点的四边形为菱形?若存在,直接写出F点的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农场要建一个长方形的养鸡场,鸡场的一边靠长为18m的墙,另三边用木栏围城,木栏长为32m.

(1)鸡场的面积能围成120m2吗?
(2)鸡场的面积能围成130m2吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AC=6![]() ,点D为直线AB上一点,且AB=3BD,直线CD与直线BC所夹锐角的正切值为
,点D为直线AB上一点,且AB=3BD,直线CD与直线BC所夹锐角的正切值为![]() ,并且CD⊥AC,则BC的长为________.
,并且CD⊥AC,则BC的长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
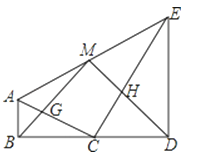
【题目】已知:如图,Rt△CDE中,∠ABC=∠CDE=90°,且BC与CD共线,联结AE,点M为AE中点,联结BM,交AC于点G,联结MD,交CE于点H
(1)求证:MB=MD;
(2)当AB=BC,DC=DE时,求证:四边形MGCH为矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
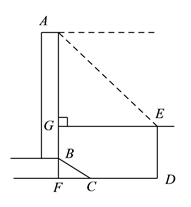
【题目】如图所示,某办公大楼正前方有一根高度是![]() 米的旗杆
米的旗杆![]() ,从办公楼顶端
,从办公楼顶端![]() 测得旗杆顶端
测得旗杆顶端![]() 的俯角
的俯角![]() 是
是![]() ,旗杆底端
,旗杆底端![]() 到大楼前梯坎底边的距离
到大楼前梯坎底边的距离![]() 是
是![]() 米,梯坎坡长
米,梯坎坡长![]() 是
是![]() 米,梯坎坡度
米,梯坎坡度![]() ,求大楼
,求大楼![]() 的高度.(精确到
的高度.(精确到![]() 米,参与数据:
米,参与数据: ![]() ,
, ![]() ,
, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某篮球队运动员进行3分球投篮成绩测试,每人每天投3分球10次,对甲、乙两名队员在5天中进球的个数统计如果如下:队员每人每天进球数(个)经过计算,甲进球的平均数为x甲=8和方差S2甲=3.2.

(1)求乙进球的平均数x乙和方差S2乙;
(2)现在需要根据以上数据,从甲、乙二人中选出一人去参加3分球投篮大赛,你认为应该选哪名队员?说说你的理由?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com