
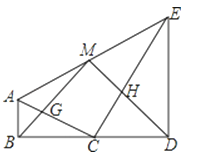
【题目】已知:如图,Rt△CDE中,∠ABC=∠CDE=90°,且BC与CD共线,联结AE,点M为AE中点,联结BM,交AC于点G,联结MD,交CE于点H
(1)求证:MB=MD;
(2)当AB=BC,DC=DE时,求证:四边形MGCH为矩形.
【答案】(1)详见解析;(2)详见解析
【解析】
(1)延长BM交DE的延长线于N,如图,根据平行线分线段成比例定理,由AB∥DN得到![]() =
=![]() ,加上AM=ME,则BM=MN,然后根据直角三角形斜边上的中线性质即可得到MB=MD;
,加上AM=ME,则BM=MN,然后根据直角三角形斜边上的中线性质即可得到MB=MD;
(2)根据平行线分线段成比例定理,由AB∥NE得到![]() =
=![]() =1,即AB=NE,再利用AB=BC,DC=DE可得BD=DN,则△BDN为等腰直角三角形,所以DM⊥BN,∠DBN=∠N=45°,∠BMD=90°,接着由Rt△ABC和Rt△CDE都是等腰直角三角形得到∠CED=∠ACB=∠45°,则可得到CE∥BN,AC∥DM,于是可判断四边形MGCH为平行四边形,加上∠GMH=90°,则可判断四边形MGCH为矩形.
=1,即AB=NE,再利用AB=BC,DC=DE可得BD=DN,则△BDN为等腰直角三角形,所以DM⊥BN,∠DBN=∠N=45°,∠BMD=90°,接着由Rt△ABC和Rt△CDE都是等腰直角三角形得到∠CED=∠ACB=∠45°,则可得到CE∥BN,AC∥DM,于是可判断四边形MGCH为平行四边形,加上∠GMH=90°,则可判断四边形MGCH为矩形.
证明:(1)延长BM交DE的延长线于N,如图,
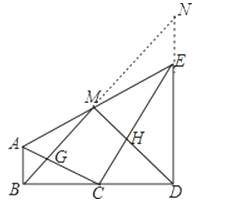
∵∠ABC=∠CDE=90°,
∴AB∥DN,
∴![]() =
=![]() ,
,
而点M为AE中点,
∴AM=ME,
∴BM=MN,
∴DM为Rt△BDN的斜边上的中线,
∴MB=MD;
(2)∵AB∥NE,
∴![]() =
=![]() =1,即AB=NE,
=1,即AB=NE,
∵AB=BC,DC=DE,
∴BD=BC+CD=AB+DE=NE+DE=DN,
∴△BDN为等腰直角三角形,
∴DM⊥BN,∠DBN=∠N=45°,∠BMD=90°,
∵AB=BC,DC=DE,
∴Rt△ABC和Rt△CDE都是等腰直角三角形,
∴∠CED=∠ACB=∠45°,
∴∠CED=∠N,∠ACB=∠BDM,
∴CE∥BN,AC∥DM,
∴四边形MGCH为平行四边形,
而∠GMH=90°,
∴四边形MGCH为矩形.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案科目:初中数学 来源: 题型:
【题目】已知关于![]() 的一元二次方程
的一元二次方程![]() 与
与![]() ,下列判断不正确的是( )
,下列判断不正确的是( )
A.若方程![]() 有两个实数根,则方程
有两个实数根,则方程![]() 也有两个实数根;
也有两个实数根;
B.如果![]() 是方程
是方程![]() 的一个根,那么
的一个根,那么![]() 是
是![]() 的一个根;
的一个根;
C.如果方程![]() 与
与![]() 有一个根相等,那么这个根是1;
有一个根相等,那么这个根是1;
D.如果方程![]() 与
与![]() 有一个根相等,那么这个根是1或-1.
有一个根相等,那么这个根是1或-1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一堂数学实践课上,赵老师给出了下列问题:
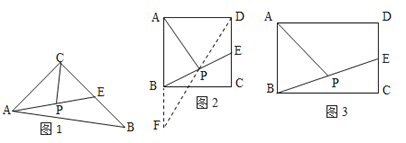
提出问题
(1)如图1,在△ABC中,E是BC的中点,P是AE的中点,就称CP是△ABC的“双中线”,∠ACB=900,AC=3,AB=5.则CP=___;
探究规律
(2)在图2中,E是正方形ABCD一边上的中点,P是BE上的中点,则称AP是正方形ABCD的“双中线”,若AB=4.则AP的长为_____;
(3)在图3中,AP是矩形ABCD的“双中线”, 若AB=4,BC=6,请仿照(2)中的方法求出AP的长,并说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某货站传送货物的平面示意图.为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°.已知原传送带AB长为4![]() 米.
米.
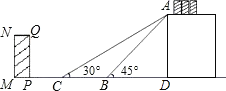
(1)求新传送带AC的长度.
(2)如果需要在货物着地点C的左侧留出2米的通道,试判断距离B点5米的货物MNQP是否需要挪走,并说明理由.
参考数据:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.为了了解全国中学生每天体育锻炼的时间,应采用普查的方式
B.若甲组数据的方差s![]() =0.03,乙组数据的方差是s
=0.03,乙组数据的方差是s![]() =0.2,则乙组数据比甲组数据稳定
=0.2,则乙组数据比甲组数据稳定
C.广安市明天一定会下雨
D.一组数据4、5、6、5、2、8的众数是5
查看答案和解析>>
科目:初中数学 来源: 题型:
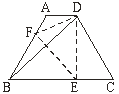
【题目】如图,等腰梯形ABCD中,AD∥BC,∠DBC=45°,翻折梯形ABCD,使点B重合于点D,折痕分别交边AB、BC于点F、E,若AD=2,BC=8.则(1)BE的长为_________. (2)∠CDE的正切值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为A(0,a),B(b,a),且a,b满足(a﹣3)2+|b﹣6|=0,现同时将点A,B分别向下平移3个单位,再向左平移2个单位,分别得到点A,B的对应点C,D,连接AC,BD,AB.

(1)求点C,D的坐标及四边形ABDC的面积S四边形ABCD;
(2)在y轴上是否存在一点M,连接MC,MD,使S△MCD=![]() S四边形ABCD?若存在这样一点,求出点M的坐标,若不存在,试说明理由;
S四边形ABCD?若存在这样一点,求出点M的坐标,若不存在,试说明理由;
(3)点P是直线BD上的一个动点,连接PA,PO,当点P在BD上移动时(不与B,D重合),直接写出∠BAP,∠DOP,∠APO之间满足的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com