
 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论中正确结论的个数是( )
如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论中正确结论的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 由正方形和折叠的性质得出AF=AB,∠B=∠AFG=90°,由HL即可证明Rt△ABG≌Rt△AFG,得出①正确;
设BG=x,则CG=BC-BG=6-x,GE=GF+EF=BG+DE=x+2,由勾股定理求出x=3,得出②正确;
由等腰三角形的性质和外角关系得出∠AGB=∠FCG,证出平行线,得出③正确;
求出△FGC的面积=$\frac{18}{5}$,得出④错误.
解答 解:∵四边形ABCD是正方形,
∴AB=AD=DC=6,∠B=D=90°,
∵CD=3DE,
∴DE=2,
∵△ADE沿AE折叠得到△AFE,
∴DE=EF=2,AD=AF,∠D=∠AFE=∠AFG=90°,
∴AF=AB,
∵在Rt△ABG和Rt△AFG中,$\left\{\begin{array}{l}{AG=AG}\\{AB=AF}\end{array}\right.$,
∴Rt△ABG≌Rt△AFG(HL),
∴①正确;
∵Rt△ABG≌Rt△AFG,
∴BG=FG,∠AGB=∠AGF,
设BG=x,则CG=BC-BG=6-x,GE=GF+EF=BG+DE=x+2,
在Rt△ECG中,由勾股定理得:CG2+CE2=EG2,
∵CG=6-x,CE=4,EG=x+2
∴(6-x)2+42=(x+2)2
解得:x=3,
∴BG=GF=CG=3,
∴②正确;
∵CG=GF,
∴∠CFG=∠FCG,
∵∠BGF=∠CFG+∠FCG,
又∵∠BGF=∠AGB+∠AGF,
∴∠CFG+∠FCG=∠AGB+∠AGF,
∵∠AGB=∠AGF,∠CFG=∠FCG,
∴∠AGB=∠FCG,
∴AG∥CF,
∴③正确;
∵△CFG和△CEG中,分别把FG和GE看作底边,
则这两个三角形的高相同.
∴$\frac{{S}_{△CFG}}{{S}_{△CEG}}$=$\frac{FG}{GE}$=$\frac{3}{5}$,
∵S△GCE=$\frac{1}{2}$×3×4=6,
∴S△CFG=$\frac{3}{5}$×6=$\frac{18}{5}$,
∴④错误;
正确的结论有3个,
故选:C.
点评 本题考查了正方形性质、折叠性质、全等三角形的性质和判定、等腰三角形的性质和判定、平行线的判定等知识点的运用;主要考查学生综合运用性质进行推理论证与计算的能力,有一定难度.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:选择题

| A. | 6 | B. | 4 | C. | 3 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
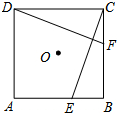 如图,E、F分别是正方形ABCD的边AB、BC上的点,BE=CF,连接CE、DF.△CDF可以看作是将△BCE绕正方形ABCD的中心O按逆时针方向旋转得到.则旋转角度为( )
如图,E、F分别是正方形ABCD的边AB、BC上的点,BE=CF,连接CE、DF.△CDF可以看作是将△BCE绕正方形ABCD的中心O按逆时针方向旋转得到.则旋转角度为( )| A. | 45° | B. | 60° | C. | 90° | D. | 120° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
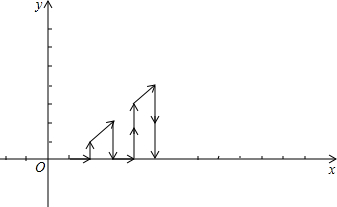 如图,在平面直角坐标系中,有若干个横坐标和纵坐标都是整数的点,其顺序排列规律如下:(1,0),(2,0),(2,1),(3,2),(3,1),(3,0),…,根据这个规律探究可得,第100个点的坐标为(14,8);第2015个点的坐标(63,3).
如图,在平面直角坐标系中,有若干个横坐标和纵坐标都是整数的点,其顺序排列规律如下:(1,0),(2,0),(2,1),(3,2),(3,1),(3,0),…,根据这个规律探究可得,第100个点的坐标为(14,8);第2015个点的坐标(63,3).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 甲乙两车分别从M,N两地相向而行,甲车出发1小时后乙车出发,并以各自的速度匀速行驶,两车相遇后依然按照原速度原方向各自行驶,如图所示是甲乙两车之间的路程S(千米)与甲车所用时间t(小时)之间的函数图象,其中D点表示甲车到达B地停止行驶.下列说法:①A,B两地路程是560千米;②乙车的速度是100千米/小时;③a=$\frac{1100}{3}$;④乙车出发3小时与甲车相遇,其中正确的个数为( )
甲乙两车分别从M,N两地相向而行,甲车出发1小时后乙车出发,并以各自的速度匀速行驶,两车相遇后依然按照原速度原方向各自行驶,如图所示是甲乙两车之间的路程S(千米)与甲车所用时间t(小时)之间的函数图象,其中D点表示甲车到达B地停止行驶.下列说法:①A,B两地路程是560千米;②乙车的速度是100千米/小时;③a=$\frac{1100}{3}$;④乙车出发3小时与甲车相遇,其中正确的个数为( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com