
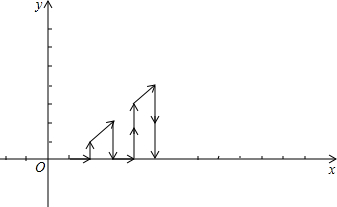
 如图,在平面直角坐标系中,有若干个横坐标和纵坐标都是整数的点,其顺序排列规律如下:(1,0),(2,0),(2,1),(3,2),(3,1),(3,0),…,根据这个规律探究可得,第100个点的坐标为(14,8);第2015个点的坐标(63,3).
如图,在平面直角坐标系中,有若干个横坐标和纵坐标都是整数的点,其顺序排列规律如下:(1,0),(2,0),(2,1),(3,2),(3,1),(3,0),…,根据这个规律探究可得,第100个点的坐标为(14,8);第2015个点的坐标(63,3). 分析 横坐标为1的点有1个,纵坐标只是0;横坐标为2的点有2个,纵坐标是0或1;横坐标为3的点有3个,纵坐标分别是0,1,2…横坐标为奇数,纵坐标从大数开始数;横坐标为偶数,则从0开始数.并且横坐标的数目与横坐标上点的个数相符,奇数列从上往下数,偶数列反之,得到接近2013个点的点所在的列数,进而判断第2015个点的坐标即可.
解答 解:∵1+2+3+…+13=91,
∴第91个点的坐标为(13,0),
∵在第14行点的走向为向上,
∴第100个点在此行上,横坐标就为14,纵坐标为从第92个点向上数8个点,即为8;
则第100个点的坐标为(14,8),
同理可求出第2013个点的坐标为(63,3),
故答案为:(14,8),(63,3).
点评 此题考查了学生的观察图形的能力和理解能力,解此题的关键是根据图形得出规律,题目比较典型,但是一道比较容易出错的题目.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
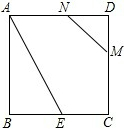 如图,正方形ABCD的边长为2,BE=CE,MN=1,线段MN的两端点在CD、AD上滑动,当DM为( )时,△ABE与以D、M、N为顶点的三角形相似.
如图,正方形ABCD的边长为2,BE=CE,MN=1,线段MN的两端点在CD、AD上滑动,当DM为( )时,△ABE与以D、M、N为顶点的三角形相似.| A. | $\frac{{\sqrt{5}}}{5}$ | B. | $\frac{{2\sqrt{5}}}{5}$ | C. | $\frac{{\sqrt{5}}}{5}$或$\frac{{2\sqrt{5}}}{5}$ | D. | $\frac{{2\sqrt{5}}}{5}$或$\frac{{3\sqrt{5}}}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论中正确结论的个数是( )
如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论中正确结论的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 某市一周平均气温(℃)如图所示,下列说法不正确的是( )
某市一周平均气温(℃)如图所示,下列说法不正确的是( )| A. | 星期二的平均气温最高 | B. | 星期四到星期日天气逐渐转暖 | ||
| C. | 这一周最高气温与最低气温相差4℃ | D. | 星期四的平均气温最低 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
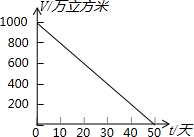 2007年的夏天,湖南省由于持续高温和连日无雨,水库蓄水量普遍下降,如图是某水库的蓄水量V(万立方米)与干旱持续时间t(天)之间的关系图,请根据此图,回答下列问题:
2007年的夏天,湖南省由于持续高温和连日无雨,水库蓄水量普遍下降,如图是某水库的蓄水量V(万立方米)与干旱持续时间t(天)之间的关系图,请根据此图,回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
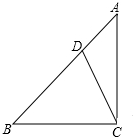 如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连接CD,
如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连接CD,查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com