
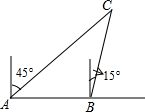
 如图所示,在一条笔直的公路旁有A,B两个公交站台相距800米,居民区C位于A站台的北偏东45°方向,位于B站台的北偏东15°方向.
如图所示,在一条笔直的公路旁有A,B两个公交站台相距800米,居民区C位于A站台的北偏东45°方向,位于B站台的北偏东15°方向.分析 (1)作BM⊥AC,垂足为M.先解直角三角形ABM,利用已知角∠MAB的正弦值,以及AB的长,可求出AM、BM.再解直角三角形BCM中,求出CM,那么根据AC=AM+CM即可求解;
(2)过点C作CD⊥AB于点D,由△ACD是等腰直角三角形可得CD=$\frac{\sqrt{2}}{2}$AC,将(1)中所求AC的值代入计算即可.
解答 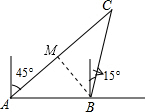 解:(1)作BM⊥AC,垂足为M.
解:(1)作BM⊥AC,垂足为M.
在直角三角形ABM中,∵∠AMB=90°,∠BAM=45°,AB=800米,
∴AM=BM=$\frac{\sqrt{2}}{2}$AB=400$\sqrt{2}$米,
在Rt△BMC中,∵∠CMB=90°,∠MBC=45°+15°=60°,
∴CM=$\sqrt{3}$BM=400$\sqrt{6}$米, ∴AC=AM+CM=(400$\sqrt{2}$+400$\sqrt{6}$)米;
∴AC=AM+CM=(400$\sqrt{2}$+400$\sqrt{6}$)米;
(2)如图,过点C作CD⊥AB于点D,
在直角三角形ACD中,
∵∠ADC=90°,∠CAD=45°,AC=(400$\sqrt{2}$+400$\sqrt{6}$)米,
∴CD=$\frac{\sqrt{2}}{2}$AC=(400+400$\sqrt{3}$)米.
点评 本题考查解直角三角形的应用-方向角问题,难度适中,解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com