
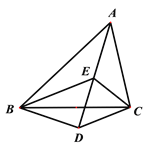
����Ŀ��С����ѧ�������εĽ�ƽ���ߺ���������4����������������������ͼ���ڡ�ABC�У���BAC= 50�㣬��I����ABC����ACBƽ���ߵĽ��㣮

����(1)����գ���BIC��_________�㣮
����(2)������D���������ƽ���ߵĽ��㣬����BDC��_________�㣮
����(3)������E���ڽ���ABC�������ACG��ƽ���ߵĽ��㣬����BEC����BAC��������ϵ��________��
����(4)�������⣨3���������£�����ACB����__________��ʱ��CE��AB��
���𰸡� 115 65 ��BEC![]() ��BAC�����BAC=2��BEC 80
��BAC�����BAC=2��BEC 80
��������������(1)�����ݽ�ƽ���ߵ������Լ��������ڽǺͶ����ó��𰸣�(2)��������������ǵ������Լ��������ڽǺͶ����ó�����֮��Ĺ�ϵ���Ӷ��ó��𰸣�(3)�����������ε��ڽǺͶ����ó��𰸣�(4)������ƽ���ߵ����ʵó���ACE=��A=50����Ȼ����ݽ�ƽ���ߵ����ʵó���ACG=2��ACE=100����Ȼ������������ڽǺͶ����ó��𰸣�
��⣺��1���ߵ�I������B��Cƽ���ߵĽ��㣬
���BIC=180��-����IBC+��ICB��=180��-![]() ����ABC+��ACB��=180��-
����ABC+��ACB��=180��-![]() ��180��-��A��
��180��-��A��
=90+![]() ��BAC=115�㣻
��BAC=115�㣻
��2����BE��BD�ֱ�Ϊ��ABC���ڽǡ����ƽ���ߣ� ���DBI=90�㣬ͬ����DCI=90�㣬
���ı���CDBI�У���BDC=180��-��BIC=90��-![]() ��BAC=65�㣻
��BAC=65�㣻
��3����BEC=![]() ��BAC��
��BAC��
֤�����ڡ�BDE�У���DBI=90�㣬���BEC=90��-��BDC=90��-��90��-![]() ��BAC��=
��BAC��=![]() ��BAC��
��BAC��
��4������ACB����80��ʱ��CE��AB���������£�
��CE��AB�����ACE=��A=50�㣬��CE�ǡ�ACG��ƽ���ߣ����ACG=2��ACE=100�㣬
���ABC=��ACG-��BAC=100��-50��=50�㣬 ���ACB=180��-��BAC-��ABC=80�㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� �������⣺����ȵĽ��ǶԶ��ǣ�������ֱ�߱�������ֱ�����أ�ͬ���ڽǻ�������ֱ����һ�㵽����ֱ�ߵĴ��߶ν����㵽ֱ�ߵľ��룻��ƽ����ͬһֱ�ߵ���ֱ����ƽ�У����м�����ĸ����ǣ�������
A.1B.2C.3D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���ı���![]() �У���A=��C=90�㣮
�У���A=��C=90�㣮
��1����ͼ1����BEƽ����ABC��DFƽ����ADC���ڲ��ǣ���д��BE��DF��λ�ù�ϵ����֤����

��2����ͼ2����BF��DE�ֱ�ƽ����ABC����ADC���ڲ��ǣ��ж�DE��BFλ�ù�ϵ��֤����

��3����ͼ3����BE��DE�ֱ���ȷ���ABC����ADC���ڲ��ǣ�����CDE=![]() ����CBE=
����CBE=![]() ��������E= ��
��������E= ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�����ǰ���ͼ1�ڷ�,��C=��DFE=90,��B=30,��E=45,��F��BC��,��A��DF��,��AFƽ�֡�CAB,�ֽ����ǰ�DFE�Ƶ�F˳ʱ����ת(����D��������FB��ʱֹͣ��ת).
(1)����AFD=_ __ʱ,DF��AC;����AFD=__ _ʱ��DF��AB��
(2)����ת�����У�DF��AB�Ľ����ΪP����ͼ2����AFP�������ڽ���ȣ����APD�Ķ�����
(3)����DE���AB��BC�ֱ��ڵ�M��Nʱ����ͼ3������AFM=2��BMN���Ƚϡ�FMN���FNM�Ĵ�С����˵�����ɡ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���BAC=60�㣬��ABC����ACB��ƽ���߽���E��D��AE�ӳ�����һ�㣬�ҡ�BDC=120�������н��ۣ��١�BEC=120�㣻��DB=DC����DB=DE;�ܡ�BDE=��BCA��������ȷ���۵ĸ���Ϊ�� ����
A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�� ��ABC����ACB�����ȷ��߽��ڵ�E��D������BFC=132�㣬��BGC=118�㣬���A�Ķ���Ϊ�� ��

A. 65�� B. 66�� C. 70�� D. 78��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ɱ߳�Ϊ1����λ���ȵ�С��������ɵ�����ͼ��
��1������ͼ�н���ƽ��ֱ������ϵ��ʹA��B���������ֱ�ΪA��2��3����B��-2��0����
��2�������������У�ÿ��С�����εĶ����Ϊ��㣬�Ը��Ϊ����������ν�����������Σ���ͼ�л��������ABCʹ��AB=AC����д���ڣ�1������������ϵ���������������ĵ�C�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(10��)��֪��ABC�ǵȱ������Σ���D��ֱ��BC��һ�㣬��ADΪһ����AD���Ҳ����ȱߡ�ADE.
(1)��ͼ�٣���D���߶�BC���ƶ�ʱ��ֱ��д����BAD�͡�CAE�Ĵ�С��ϵ��
(2)��ͼ�ڣ���D���߶�BC���ӳ������ƶ�ʱ�������DCE�Ĵ�С�Ƿ����仯����������������С�����仯����˵�����ɣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com