
����Ŀ��һ�����ǰ���ͼ1�ڷ�,��C=��DFE=90,��B=30,��E=45,��F��BC��,��A��DF��,��AFƽ�֡�CAB,�ֽ����ǰ�DFE�Ƶ�F˳ʱ����ת(����D��������FB��ʱֹͣ��ת).
(1)����AFD=_ __ʱ,DF��AC;����AFD=__ _ʱ��DF��AB��
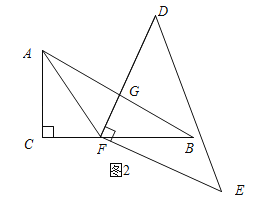
(2)����ת�����У�DF��AB�Ľ����ΪP����ͼ2����AFP�������ڽ���ȣ����APD�Ķ�����
(3)����DE���AB��BC�ֱ��ڵ�M��Nʱ����ͼ3������AFM=2��BMN���Ƚϡ�FMN���FNM�Ĵ�С����˵�����ɡ�

���𰸡�(1)30��60(2) 60��105��150(3)��FMN=��FNM
����������������1������AFD=30��ʱ��AC��DF�����ݽ�ƽ���ߵĶ��������á�CAF=��FAB=30�㣬���ڴ����������ֱ��ƽ������֤��AC��DF��������AFD=60��ʱ��DF��AB���������ε��ڽǺͶ���֤��������
��2����Ϊ��FAP=��AFP����AFP=��APF����APF=��FAP���������⼴����
��3����������������ǵ�����֤����FNM=30��+��BMN����������������������ǵ������Լ���AFM�͡�BMN�Ĺ�ϵ��֤����FMN=30��+��BMN���Ӷ��ɵõ���FNM���FMN�Ĺ�ϵ��
�������1����ͼ1��ʾ��
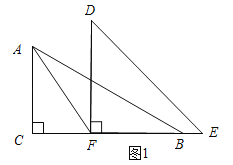
����AFD=30ʱ��AC��DF��
�������ߡ�CAB=60�㣬AFƽ�֡�CAB�����CAF=30�㣮
�ߡ�AFD=30�㣬���CAF=��AFD����AC��DF��
��ͼ2��ʾ������AFD=60��ʱ��DF��AB��
�ߡ�CAB=60�㣬AFƽ�֡�CAB�����AFG=30�㣮
�ߡ�AFD=60�㣬���FGB=90�㣬��DF��AB��
�ʴ�Ϊ��30��60��
��2���ߡ�CAB=60�㣬AFƽ�֡�CAB�����FAP=30�㣮
����ͼ3��ʾ��
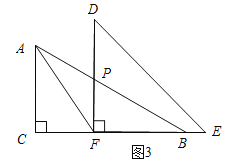
����FAP=��AFP=30��ʱ����APD=��FAP+��AFP=30��+30��=60�㣻
��ͼ4��ʾ��

����AFP=��APFʱ��
�ߡ�FAP=30�㣬��AFP=��APF�����AFP=��APF=![]() ����180�㩁30�㣩=
����180�㩁30�㣩=![]() ��150��=75�㣬���APD=��FAP+��AFP=30��+75��=105�㣻
��150��=75�㣬���APD=��FAP+��AFP=30��+75��=105�㣻
��ͼ5��ʾ��
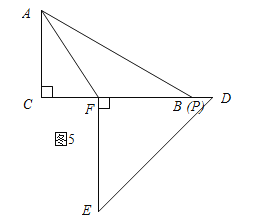
��ͼ5��ʾ������APF=��FAP=30��ʱ��
��APD=180�㩁30��=150�㣮
������������APD�Ķ���Ϊ60����105����150�㣮
��3����FMN=��FNM��
��������ͼ6��ʾ��

�ߡ�FNM�ǡ�BMN��һ����������FNM=��B+��BMN��
�ߡ�B=30�㣬���FNM=��B+��BMN=30��+��BMN��
�ߡ�BMF�ǡ�AFM��һ����������MBF=��MAF+��AFM������BMN+��FMN=��MAF+��AFM��
�֡ߡ�MAF=30�㣬��AFM=2��BMN�����BMN+��FMN=30��+2��BMN�����FMN=30��+��BMN�����FNM=��FMN��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����µ����У����˳���������ǣ� ��
A.�˽�ij��ѧ�����������
B.����ij���������Ŀ�ײ������
C.�˽�ȫ��ͬѧÿ������������ʱ��
D.��ijУ�����꼶��2����ѧ�����ܲ��Դ������ĵ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����е��飺
���˽�ij�����ӵķ�ѿ�� ���˽�ij��ѧ���ԡ����������ļ�ֵ�ۡ���֪����
���˽�ij��������ˮˮ�� ���˽����꼶��1����ѧ���μӡ������Կ�ѧʵ�������ɴ���
�ʺϲ�ȡȫ�������ǣ� ��
A.�٢�B.�ڢ�C.�٢�D.�ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������У�ÿ��С�����εı߳���Ϊ1����λ���ȣ���ABC�����������λ����ͼ��ʾ���ֽ���ABCƽ�ƣ�ʹ��A�任Ϊ��D����E��F�ֱ���B��C�Ķ�Ӧ�㣮
��1���뻭��ƽ�ƺ�ġ�DEF��
��2��������AD��CF�����������߶�֮�����ϵ��________________��
��3����ͼ���ҳ���������S��ABC��S��QBC�ĸ��Q (���ڵ�A)������Q1��Q2����ʾ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����ѧ�������εĽ�ƽ���ߺ���������4����������������������ͼ���ڡ�ABC�У���BAC= 50�㣬��I����ABC����ACBƽ���ߵĽ��㣮

����(1)����գ���BIC��_________�㣮
����(2)������D���������ƽ���ߵĽ��㣬����BDC��_________�㣮
����(3)������E���ڽ���ABC�������ACG��ƽ���ߵĽ��㣬����BEC����BAC��������ϵ��________��
����(4)�������⣨3���������£�����ACB����__________��ʱ��CE��AB��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��y�ķ�����![]() �Ľ�����x��0��y��0��
�Ľ�����x��0��y��0��
��1��x��________, y��________���ú�a�Ĵ���ʽ��ʾ����
��2����a��ȡֵ��Χ��
��3����2x8y=2m���ú���a�Ĵ���ʽ��ʾm������m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ķ���������ݣ��ٽ������.
���⣺��![]() , ��m��n��ֵ
, ��m��n��ֵ
�⣺��![]()
��![]()
��![]()
��![]() ��
�� ![]()
��![]() ��
�� ![]()
���⣺(1)��![]() ����
����![]() ��ֵ��
��ֵ��
(2)��֪a��b��c�ǡ�ABC�����߳�������![]() ,��c�ǡ�ABC����ıߣ���c��ȡֵ��Χ��
,��c�ǡ�ABC����ıߣ���c��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com