【题目】如图，在矩形ABCD中，已知AB=4，BC=3，矩形在直线l上绕其右下角的顶点B向右旋转90°至图①位置，再绕右下角的顶点继续向右旋转90°至图②位置，…，以此类推，这样连续旋转2016次后，顶点A在整个旋转过程中所经过的路程之和是（ ）
A.2015π
B.3019.5π
C.3018π
D.3024π
出彩同步大试卷系列答案科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，直线y＝﹣x+8分别交两轴于点A、B，点C的横坐标为4，点D在线段OA上，且AD＝7．
（1）求直线CD的解析式；
（2）P为直线CD上一点，若△PAB面积为20，求P的坐标；
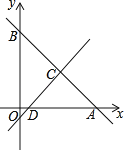
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】发现与探索：你能求（x﹣1）（x2019+x2018+x2017+……+x+1）的值吗？遇到这样的问题，我们可以先思考一下，从简单的情形入手．先分别计算下列各式的值：
（1）（x﹣1）（x+1）＝x2﹣1；
（2）（x﹣1）（x2+x+1）＝x3﹣1；
（3）（x﹣1）（x3+x2+x+1）＝x4﹣1；
……
由此我们可以得到：（x﹣1）（x2019+x2018+x2017+……+x+1）＝ ；请你利用上面的结论，完成下面两题的计算：
（1）32019+32018+32017+……+3+1；
（2）（﹣2）50+（﹣2）49+（﹣2）48+……+（﹣2）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】问题情境：如图1，
，
，
，求
度数.小明的思路是：过
作
，如图2，通过平行线性质来求.
（1）按小明的思路，易求得的度数为_________；请说明理由；
问题迁移：
（2）如图3，
，点在射线
上运动，当点在
、
两点之间运动时，
，
，则
、
、
之间有何数量关系？请说明理由；
（3）在（2）的条件下，如果点在、两点外侧运动时（点与点、、
三点不重合），请你直接写出、、间的数量关系.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】计算或化简
(1)|﹣1|+(﹣2)3+(7﹣π)0﹣
(2)3a32a6﹣3a12÷a3
(3)(x+y)2+(x﹣y)(x+2y)
(4)(3a+b﹣2)(3a﹣b+2)
(5)(3a+2)2(3a﹣2)2
(6)7862﹣786×172+862
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一辆客车从甲地开往乙地，一辆出租车从乙地开往甲地，两车同时出发，设客车离甲地的距离为y1千米，出租车离甲地的距离为y2千米，两车行驶的时间为x小时，y1、y2关于x的函数图像如下图
所示：
（1）根据图像，直接写出y1、y2关于x的函数关系式；
（2）若两车之间的距离为S千米，请写出S关于x的函数关系式；
（3）甲、乙两地间有A、B两个加油站，相距200千米，若客车进入A加油站时，出租车恰好进入B加油站，求A加油站离甲地的距离.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】“化归与转化的思想”是指在研究解决数学问题时采用某种手段将问题通过变换使之转化，进而使问题得到解决。
(1)我们知道
可以得到
。如果
，求
、
的值.
(2)已知
试问多项式a2+b2+c2﹣ab﹣ac﹣bc的值是否与变量
的取值有关？若有关请说明理由；若无关请求出多项式的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知
的一条边
的长为5，另两边
的长是关于
的一元二次方程
的两个实数根．
（1）求证：无论
为何值，方程总有两个不相等的实数根；
（2）当为何值时，为直角三角形，并求出的周长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
