
ЁОЬтФПЁПМзЁЂввСНаЃВЮМгЧјНЬг§ОжОйАьЕФбЇЩњгЂгяПкгяОКШќЃЌСНаЃВЮШќШЫЪ§ЯрЕШЃЎБШШќНсЪјКѓЃЌЗЂЯжбЇЩњГЩМЈЗжБ№ЮЊ7ЗжЁЂ8ЗжЁЂ9ЗжЁЂ10ЗжЃЈТњЗжЮЊ10ЗжЃЉЃЎвРОнЭГМЦЪ§ОнЛцжЦСЫШчЯТЩаВЛЭъећЕФЭГМЦЭМБэЃЎ
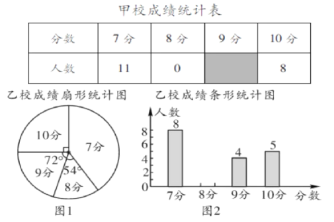
ЃЈ1ЃЉдкЭМ1жаЃЌЁА7ЗжЁБЫљдкЩШаЮЕФдВаФНЧЕШгк ЃЎ
ЃЈ2ЃЉЧыФуНЋЭМ2ЕФЬѕаЮЭГМЦЭМВЙГфЭъећЃЛ
ЃЈ3ЃЉОМЦЫуЃЌвваЃЕФЦНОљЗжЪЧ8.3ЗжЃЌжаЮЛЪ§ЪЧ8ЗжЃЌЧыаДГіМзаЃЕФЦНОљЗжЁЂжаЮЛЪ§ЃЛВЂДгЦНОљЗжКЭжаЮЛЪ§ЕФНЧЖШЗжЮіФФИібЇаЃГЩМЈНЯКУЃЎ
ЁОД№АИЁПЃЈ1ЃЉ144ЃЛЃЈ2ЃЉЬѕаЮЭГМЦЭМВЙГфМћНтЮіЃЛЃЈ3ЃЉЦНОљЗжЮЊ8.3ЃЌжаЮЛЪ§ЮЊ7ЃЌДгЦНОљЪ§ПДЃЌСНЖгГЩМЈвЛбљЃЌДгжаЮЛЪ§ПДЃЌввЖгГЩМЈКУ.
ЁОНтЮіЁП
ЃЈ1ЃЉШЯецЗжЮіЬтвтЃЌЙлВьЩШаЮЭГМЦЭМЃЌИљОнЩШаЮЭГМЦЭМЕФдВаФНЧжЎКЭЮЊ360ЁуКЭЫљИјЕФНЧЖШМДПЩЕУЕНД№АИЃЛ
ЃЈ2ЃЉНсКЯЩШаЮЭГМЦЭМКЭЬѕаЮЭГМЦЭМЃЌЕУГівваЃВЮМгЕФШЫЪ§ЃЌМДПЩЕУ8ЗжЕФШЫЪ§ЃЌЭъГЩЬѕаЮЭГМЦЭММДПЩ.
ЃЈ3ЃЉНсКЯЕкЃЈ2ЃЉЮЪЕФД№АИЃЌПЩвдВЙГфЭГМЦБэЃЌНгЯТРДНсКЯЦНОљЪ§ЁЂжаЮЛЪ§ЕФИХФюЃЌМДПЩЧѓГіМзаЃЕФЦНОљЗжвдМАжаЮЛЪ§ЃЌЭЈЙ§гывваЃНјааБШНЯЃЌМДПЩЕУЕНД№АИ.
ЃЈ1ЃЉЙлВьЩШаЮЭГМЦЭМЃЌПЩЕУ
ЁА7ЗжЁБЫљдкЩШаЮЭМЕФдВаФНЧЕШгк360Ёу-(90Ёу+54Ёу+72Ёу)=144Ёу
ЃЈ2ЃЉ![]() ЃЈШЫЃЉ
ЃЈШЫЃЉ
20-8-4-5=3ЃЈШЫЃЉ
вваЃЕУ8ЗжЕФШЫЪ§ЮЊ3ЃЌВЙГфЭГМЦЭМШчЭМЫљЪО

ЃЈ3ЃЉгЩМзввСНаЃВЮМгЕФШЫЪ§ЯрЕШЃЌПЩЕУ
МзаЃЕУ9ЗжЕФШЫЪ§ЮЊ20-(11+8)=1
ЙЪМзаЃГЩМЈЭГМЦБэжаЃЌЕУ9ЗжЕФЖдгІШЫЪ§ЮЊ1.
НсКЯЦНОљЪ§ЕФИХФюЃЌПЩЕУ
МзаЃЕФЦНОљЗжЮЊ![]() =8.3ЃЈЗжЃЉ
=8.3ЃЈЗжЃЉ
НсКЯжаЮЛЪ§ЕФИХФюЃЌПЩЕУ
МзаЃЕФжаЮЛЪ§ЮЊ7
ДгЦНОљЗжЁЂжаЮЛЪ§ЕФНЧЖШЗжЮіЃЌМзввСНаЃЕФЦНОљЗжЯрЭЌЃЌвваЃЕФжаЮЛЪ§ЃОМзаЃЕФжаЮЛЪ§ЃЌ
ПЩжЊвваЃЕФГЩМЈКУ.


 ЦпаЧЭМЪщПкЫуЫйЫуЬьЬьСЗЯЕСаД№АИ
ЦпаЧЭМЪщПкЫуЫйЫуЬьЬьСЗЯЕСаД№АИ ГѕжабЇвЕПМЪдЕМгыСЗЯЕСаД№АИ
ГѕжабЇвЕПМЪдЕМгыСЗЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙцЖЈЃКЧѓШєИЩИіЯрЭЌЕФгаРэЪ§ЃЈОљВЛЕШгк ![]() ЃЉЕФГ§ЗЈдЫЫуНазіГ§ЗНЃЌШч
ЃЉЕФГ§ЗЈдЫЫуНазіГ§ЗНЃЌШч ![]() ЃЌ
ЃЌ ![]() ЕШЃЌРрБШгаРэЪ§ГЫЗНЃЌЮвУЧАб
ЕШЃЌРрБШгаРэЪ§ГЫЗНЃЌЮвУЧАб ![]() МЧзї
МЧзї ![]() ЃЌЖСзїЁА
ЃЌЖСзїЁА ![]() ЕФШІ
ЕФШІ ![]() ДЮЗНЃЌЁБ
ДЮЗНЃЌЁБ ![]() МЧзї
МЧзї ![]() ЃЌЖСзїЃКЁА
ЃЌЖСзїЃКЁА ![]() ЕФШІ
ЕФШІ ![]() ДЮЗНЁБ.вЛАуЕиЃЌАб
ДЮЗНЁБ.вЛАуЕиЃЌАб ![]() МЧзїa ЃЌ ЖСзїЁА
МЧзїa ЃЌ ЖСзїЁА ![]() ЕФШІ
ЕФШІ ![]() ДЮЗНЁБ
ДЮЗНЁБ
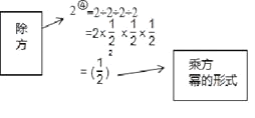
ЃЈ1ЃЉЃЈГѕВНЬНОПЃЉ
Ђё.жБНгаДГіМЦЫуНсЙћЃК ![]() =________ЃЌ
=________ЃЌ ![]() ________.
________.
Ђђ.ЙигкГ§ЗНЃЌЯТСаЫЕЗЈДэЮѓЕФЪЧЃЈ________ЃЉ
A.ШЮКЮЗЧСуЪ§ЕФШІ ![]() ДЮЗНЖМЕШгкЫќЕФЕЙЪ§
ДЮЗНЖМЕШгкЫќЕФЕЙЪ§
B.СНИіЪ§ЛЅЮЊЕЙЪ§ЃЌФЧУДЫќЕФnДЮЗНКЭШІnДЮЗНвВЛЅЮЊЕЙЪ§
C.ЖдгкШЮКЮе§ећЪ§ ![]() ЃЌ(-1)=1
ЃЌ(-1)=1
D.ИКЪ§ЕФШІЦцЪ§ДЮЗННсЙћЪЧИКЪ§ЃЌИКЪ§ЕФШІХМЪ§ДЮЗННсЙћЪЧе§Ъ§.
ЃЈ2ЃЉЃЈЩюШыЫМПМЃЉ
ЮвУЧжЊЕРЃЌгаРэЪ§ЕФМѕЗЈдЫЫуПЩвдзЊЛЏЮЊМгЗЈдЫЫуЃЌГ§ЗЈдЫЫуПЩвдзЊЛЏЮЊГЫЗЈдЫЫуЃЌгаРэЪ§ЕФГ§ЗНдЫЫуШчКЮзЊЛЏЮЊГЫЗНдЫЫуФиЃП
Ђё.ЪдвЛЪдЃЌЗТееЩЯУцЕФЫуЪНЃЌНЋЯТСадЫЫуНсЙћжБНгаДГЩУнЕФаЮЪН.- ![]() ________ЃЛ
________ЃЛ![]() ________.
________.
Ђђ.ЯывЛЯыЃКНЋвЛИіЗЧСугаРэЪ§ ![]() ЕФШІ /span>
ЕФШІ /span>![]() ДЮЗНаДГЩУнЕФаЮЪНЕШгк________.
ДЮЗНаДГЩУнЕФаЮЪНЕШгк________.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЦЖЏЛЅСЊЭјЪЧЯжДњЭЈаХЦНЬЈЃЌПЩвдЪЕЯжЪжЛњжЎМфЕФЫНУмЛЅСЊЃЌШЮвтСНЬЈЪжЛњЫНУмЛЅСЊЙЙГЩвЛЬѕСЌНгЭЈТЗ.
ЃЈ1ЃЉШє![]() ЬЈЪжЛњ
ЬЈЪжЛњ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЭЌЪБЫНУмЛЅСЊЃЌЧыЛГіЭМаЮЃЌВЂгУЯпЖЮБэЪОЙЙГЩЕФЫљгаСЌНгЭЈТЗЃК
ЭЌЪБЫНУмЛЅСЊЃЌЧыЛГіЭМаЮЃЌВЂгУЯпЖЮБэЪОЙЙГЩЕФЫљгаСЌНгЭЈТЗЃК
ЃЈ2ЃЉШє![]() ЬЈЪжЛњ
ЬЈЪжЛњ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЭЌЪБЫНУмЛЅСЊЃЌаЮГЩМИЬѕСЌНгЭЈТЗЃП
ЭЌЪБЫНУмЛЅСЊЃЌаЮГЩМИЬѕСЌНгЭЈТЗЃП
ЃЈ3ЃЉШє![]() ЬЈЪжЛњЭЌЪБЫНУмЛЅСЊЃЌаЮГЩМИЬѕСЌНгЭЈТЗЃПЧыгУКЌ
ЬЈЪжЛњЭЌЪБЫНУмЛЅСЊЃЌаЮГЩМИЬѕСЌНгЭЈТЗЃПЧыгУКЌ![]() ЕФЪНзгБэЪО.
ЕФЪНзгБэЪО.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
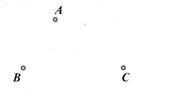
ЁОЬтФПЁПШчЭМЃЌЯрОр5kmЕФAЁЂBСНЕиМфгавЛЬѕБЪжБЕФТэТЗЃЌCЕиЮЛгкABСНЕижЎМфЧвОрAЕи2kmЃЌаЁУїЭЌбЇЦяздааГЕДгAЕиГіЗЂбиТэТЗвдУПаЁЪБ5kmЕФЫйЖШЯђBЕидШЫйдЫЖЏЃЌЕБЕНДяBЕиКѓСЂМДвддРДЕФЫйЖШЗЕЛиЁЃЕНДяAЕиЭЃжЙдЫЖЏЃЌЩшдЫЖЏЪБМфЮЊt(аЁЪБ).аЁУїЕФЮЛжУЮЊЕуPЁЂШєвдЕуCЮЊзјБъдЕуЃЌвдДгAЕНBЮЊе§ЗНЯђЃЌгУ1ИіЕЅЮЛГЄЖШБэЪО1kmЃЌНтД№ЯТСаИїЮЪЃК
![]()
(1)жИГіЕуAЫљБэЪОЕФгаРэЪ§ЃЛ
(2)Чѓt =0.5ЪБЃЌЕуPБэЪОЕФгаРэЪ§ЃЛ
(3)ЕБаЁУїОрРыCЕи1kmЪБЃЌжБНгаДГіЫљгаТњзуЬѕМўЕФtжЕЃЛ
(4)дкећИідЫЖЏЙ§ГЬжаЃЌЧѓЕуPгыЕуAЕФОрРы(гУКЌtЕФДњЪ§ЪНБэЪО)ЃЛ
(5)гУКЌtЕФДњЪ§ЪНБэЪОЕуPБэЪОЕФгаРэЪ§.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌе§ЗНаЮжНЦЌABCDжаЃЌЖдНЧЯпACЃЌBDНЛгкЕуOЃЌелЕўе§ЗНаЮжНЦЌABCDЃЌЪЙADТфдкBDЩЯЃЌЕуAЧЁКУгыBDЩЯЕФЕуFжиКЯЃЌеЙПЊКѓелКлDEЗжБ№НЛABЃЌACгкЕуEЃЌGЃЌСЌНгGFЃЌИјГіЯТСаНсТлЃК
ЂйЁЯADG=22.5ЁуЃЛЂкtanЁЯAED=2ЃЛЂлSЁїAGD=SЁїOGDЃЛЂмЫФБпаЮAEFGЪЧСтаЮЃЛЂнBE=2OGЃЛЂоШєSЁїOGF=1ЃЌдђе§ЗНаЮABCDЕФУцЛ§ЪЧ6+4![]() ЃЌЦфжае§ШЗЕФНсТлИіЪ§гаЃЈЃЉ
ЃЌЦфжае§ШЗЕФНсТлИіЪ§гаЃЈЃЉ
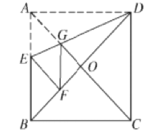
A. 2ИіB. 4ИіC. 3ИіD. 5Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬЕъзМБИНјвЛХњМОНкадаЁМвЕчЃЌУПИіНјМлЮЊ40дЊЃЌОЪаГЁдЄВтЃЌЯњЪлЖЈМлЮЊ50дЊЃЌПЩЪлГі400ИіЃЛЖЈМлУПдіМг1дЊЃЌЯњЪлСПНЋМѕЩй10ИіЃЎЩшУПИіЖЈМлдіМгxдЊЃЎ
ЃЈ1ЃЉаДГіЪлГівЛИіПЩЛёЕУЕФРћШѓЪЧЖрЩйдЊЃЈгУКЌxЕФДњЪ§ЪНБэЪОЃЉЃП
ЃЈ2ЃЉЩЬЕъШєзМБИЛёЕУРћШѓ6000дЊЃЌВЂЧвЪЙНјЛѕСПНЯЩйЃЌдђУПИіЖЈМлЮЊЖрЩйдЊЃПгІНјЛѕЖрЩйИіЃП
ЃЈ3ЃЉЩЬЕъШєвЊЛёЕУзюДѓРћШѓЃЌдђУПИігІЖЈМлЖрЩйдЊЃПЛёЕУЕФзюДѓРћШѓЪЧЖрЩйЃП
ЁОД№АИЁПЃЈ1ЃЉx+10дЊЃЛЃЈ2ЃЉУПИіЖЈМлЮЊ70дЊЃЌгІНјЛѕ200ИіЃЎЃЈ3ЃЉУПИіЖЈМлЮЊ65дЊЪБЕУзюДѓРћШѓЃЌПЩЛёЕУЕФзюДѓРћШѓЪЧ6250дЊЃЎ
ЁОНтЮіЁПЪдЬтЗжЮі:ЃЈ1ЃЉИљОнРћШѓ=ЯњЪлМл-НјМлСаЙиЯЕЪН,ЃЈ2ЃЉзмРћШѓ=УПИіЕФРћШѓЁСЯњЪлСП,ЯњЪлСПЮЊ400-10x,СаЗНГЬЧѓНт,ИљОнЬтвтШЁЩс,ЃЈ3ЃЉРћгУКЏЪ§ЕФаджЪЧѓзюжЕ.
ЪдЬтНтЮі:гЩЬтвтЕУ:ЃЈ1ЃЉ50+x-40=x+10ЃЈдЊЃЉ,
ЃЈ2ЃЉЩшУПИіЖЈМлдіМгxдЊ,
СаГіЗНГЬЮЊ:ЃЈx+10ЃЉЃЈ400-10xЃЉ=6000,НтЕУ:x1=10,x2=20,вЊЪЙНјЛѕСПНЯЩй,дђУПИіЖЈМлЮЊ70дЊ,гІНјЛѕ200Иі,
ЃЈ3ЃЉЩшУПИіЖЈМлдіМгxдЊ,ЛёЕУРћШѓЮЊyдЊ,
y=ЃЈx+10ЃЉЃЈ400-10xЃЉ=-10x2+300x+4000=-10ЃЈx-15ЃЉ2+6250,ЕБx=15ЪБ,yгазюДѓжЕЮЊ6250,ЫљвдУПИіЖЈМлЮЊ65дЊЪБЕУзюДѓРћШѓ,ПЩЛёЕУЕФзюДѓРћШѓЪЧ6250дЊ.
ЁОЬтаЭЁПНтД№Ьт
ЁОНсЪјЁП
24
ЁОЬтФПЁПВТЯыгыжЄУїЃК
ШчЭМ1ЃЌАкЗХОиаЮжНЦЌABCDгыОиаЮжНЦЌECGFЃЌЪЙBЁЂCЁЂGШ§ЕудквЛЬѕжБЯпЩЯЃЌCEдкБпCDЩЯЃЌСЌНгAFЃЌШєMЮЊAFЕФжаЕуЃЌСЌНгDMЁЂMEЃЌЪдВТЯыDMгыMEЕФЙиЯЕЃЌВЂжЄУїФуЕФНсТлЃЎ
ЭиеЙгыбгЩьЃК
ЃЈ1ЃЉШєНЋЁБВТЯыгыжЄУїЁАжаЕФжНЦЌЛЛГЩе§ЗНаЮжНЦЌABCDгые§ЗНаЮжНЦЌECGFЃЌЦфЫћЬѕМўВЛБфЃЌдђDMКЭMEЕФЙиЯЕЮЊЁЁ ЁЁЃЎ
ЃЈ2ЃЉШчЭМ2АкЗХе§ЗНаЮжНЦЌABCDгые§ЗНаЮжНЦЌECGFЃЌЪЙЕуFдкБпCDЩЯЃЌЕуMШдЮЊAFЕФжаЕуЃЌЪджЄУїЃЈ1ЃЉжаЕФНсТлШдШЛГЩСЂЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЭЌбЇУЧжЊЕРЃЌ|8Љ3|БэЪО8гы3ЕФВюЕФОјЖджЕЃЌвВПЩРэНтЮЊЪ§жсЩЯБэЪОЪ§8гы3СНЕуМфЕФОрРыЃЎЪдЬНЫїЃК
ЃЈ1ЃЉЬюПеЃК|8+3|БэЪОЪ§жсЩЯЪ§8гыЪ§ЁЁ ЁЁСНЕуМфЕФОрРыЃЛ
ЃЈ2ЃЉ|x+5|+|xЉ2|БэЪОЪ§жсЩЯЪ§xгыЪ§ЁЁ ЁЁЕФОрРыКЭЪ§xгыЪ§ЁЁ ЁЁЕФОрРыЕФКЭЃЎ
ЃЈ3ЃЉТњзу|x+5|+|xЉ2|ЃН7ЕФЫљгаећЪ§xЕФжЕЪЧЁЁ ЁЁЃЎ
ЃЈ4ЃЉгЩвдЩЯЬНЫїВТЯыЖдгкШЮКЮгаРэЪ§xЃЌ|xЉ3|+|xЉ6|ЪЧЗёгазюаЁжЕЃПШчЙћгааДГізюаЁжЕЃЛШчЙћУЛгаЃЌЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПОиаЮABCDжаЃЌCEЦНЗжЁЯBCDЃЌНЛжБЯпADгкЕуEЃЌШєCD=6ЃЌAE=2ЃЌдђtanЁЯACE=______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЪ§жсЩЯЃЌЕуAЃЌBЃЌCБэЪОЕФЪ§ЗжБ№ЪЧЃ6ЃЌ10ЃЌ12ЃЎЕуAвдУПУы3ИіЕЅЮЛГЄЖШЕФЫйЖШЯђгвдЫЖЏЃЌЭЌЪБЯпЖЮBCвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШвВЯђгвдЫЖЏЃЎ
ЃЈ1ЃЉдЫЖЏЧАЯпЖЮABЕФГЄЖШЮЊ________ЃЛ
ЃЈ2ЃЉЕБдЫЖЏЪБМфЮЊЖрГЄЪБЃЌЕуAКЭЯпЖЮBCЕФжаЕужиКЯЃП
ЃЈ3ЃЉЪдЬНОПЪЧЗёДцдкдЫЖЏЕНФГвЛЪБПЬЃЌЯпЖЮAB=![]() ACЃПШєДцдкЃЌЧѓГіЫљгаЗћКЯЬѕМўЕФЕуAБэЪОЕФЪ§ЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ACЃПШєДцдкЃЌЧѓГіЫљгаЗћКЯЬѕМўЕФЕуAБэЪОЕФЪ§ЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com