
【题目】经统计分析,某市跨河大桥上的车流速度v(千米/小时)是车流密度x(辆/千米)的函数,当桥上的车流密度达到220辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度不超过20辆/千米时,车流速度为80千米/小时,研究表明:当20≤x≤220时,车流速度v是车流密度x的一次函数.
(1)求大桥上车流密度为100辆/千米时的车流速度;
(2)在交通高峰时段,为使大桥上的车流速度大于40千米/小时且小于60千米/小时,应控制大桥上的车流密度在什么范围内?
(3)车流量(辆/小时)是单位时间内通过桥上某观测点的车辆数,即:车流量=车流速度×车流密度.求大桥上车流量y的最大值.
【答案】(1)大桥上车流密度为100辆/千米时的车流速度48千米/小时;
(2)应控制大桥上的车流密度在70<x<120范围内;
(3)当车流密度是110辆/千米,车流量y取得最大值是每小时4840辆.
【解析】
试题分析:(1)当20≤x≤220时,设车流速度v与车流密度x的函数关系式为v=kx+b,根据题意的数量关系建立方程组求出其解即可;
(2)由(1)的解析式建立不等式组求出其解即可;
(3)设车流量y与x之间的关系式为y=vx,当x<20和20≤x≤220时分别表示出函数关系由函数的性质就可以求出结论.
试题解析:(1)设车流速度v与车流密度x的函数关系式为v=kx+b,由题意,得
![]() ,
,
解得: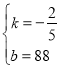 ,
,
∴当20≤x≤220时,v=﹣![]() x+88,
x+88,
当x=100时,v=﹣![]() ×100+88=48(千米/小时);
×100+88=48(千米/小时);
(2)由题意,得
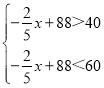 ,
,
解得:70<x<120.
∴应控制大桥上的车流密度在70<x<120范围内;
(3)设车流量y与x之间的关系式为y=vx,
当0≤x≤20时
y=80x,
∴k=80>0,
∴y随x的增大而增大,
∴x=20时,y最大=1600;
当20≤x≤220时
y=(﹣![]() x+88)x=﹣
x+88)x=﹣![]() (x﹣110)2+4840,
(x﹣110)2+4840,
∴当x=110时,y最大=4840.
∵4840>1600,
∴当车流密度是110辆/千米,车流量y取得最大值是每小时4840辆.


 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
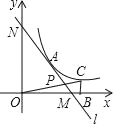
【题目】如图,在平面直角坐标系中,直线l与x轴相交于点M(3,0),与y轴相交于点N(0,4),点A为MN的中点,反比例函数y=![]() (x>0)的图象过点A.
(x>0)的图象过点A.
(1)求直线l和反比例函数的解析式;
(2)在函数y=![]() (k>0)的图象上取异于点A的一点C,作CB⊥x轴于点B,连接OC交直线l于点P,若△ONP的面积是△OBC面积的3倍,求点P的坐标.
(k>0)的图象上取异于点A的一点C,作CB⊥x轴于点B,连接OC交直线l于点P,若△ONP的面积是△OBC面积的3倍,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知多项式(2x2+ax-y+6)-(2bx22x 5y1).
(1)若多项式的值与字母x的取值无关,求a、b的值.
(2)在(1)的条件下,先化简多项式3(a-ab+b)-(a+ ab+ b),再求它的值.
(3)在(1)的条件下,求(b+a2)+(2b+![]() a2)+(3b+
a2)+(3b+![]() a2)+…+(9b+
a2)+…+(9b+![]() a2)的值.
a2)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC为直角三角形,∠C=90°,边BC是⊙O的切线,切点为D,AB经过圆心O并与圆相交于点E,连接AD.
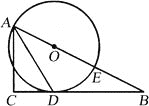
(1)求证:AD平分∠BAC;
(2)若AC=8,tan∠DAC=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线的顶点为P(﹣2,2),与y轴交于点A(0,3).若平移该抛物线使其顶点P沿直线移动到点P′(2,﹣2),点A的对应点为A′,则抛物线上PA段扫过的区域(阴影部分)的面积为______.
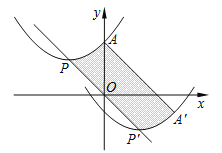
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形OABC中,BC∥AO,∠AOC=90°,点A,B的坐标分别为(5,0), (2,6),点D为AB上一点,且BD=2AD,双曲线y=![]() (k>0)经过点D,交BC于点E.
(k>0)经过点D,交BC于点E.
(1)求双曲线的解析式;
(2)求四边形ODBE的面积.
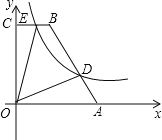
查看答案和解析>>
科目:初中数学 来源: 题型:
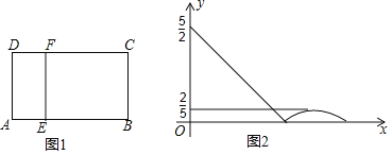
【题目】如图1,在矩形ABCD中,动点E从A出发,沿![]() 方向运动,当点E到达点C时停止运动,过点E做
方向运动,当点E到达点C时停止运动,过点E做![]() ,交CD于F点,设点E运动路程为x,
,交CD于F点,设点E运动路程为x, ![]() ,如图2所表示的是y与x的函数关系的大致图象,当点E在BC上运动时,FC的最大长度是
,如图2所表示的是y与x的函数关系的大致图象,当点E在BC上运动时,FC的最大长度是![]() ,则矩形ABCD的面积是( )
,则矩形ABCD的面积是( )
A. ![]() B.
B. ![]() C. 6 D. 5
C. 6 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正方形 ABCD (如图 1)作如下划分:
第1次划分:分别连接正方形ABCD对边的中点(如图2),得线段HF和EG,它们交于点M,此时图2中共有5个正方形;
第2次划分:将图2 左上角正方形AEMH再作划分,得图3,则图3 中共有9个正方形;
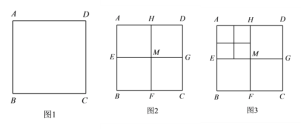
(1)若每次都把左上角的正方形依次划分下去,则第100次划分后,图中共有 个正方形;
(2)继续划分下去,第几次划分后能有805个正方形?写出计算过程.
(3)按这种方法能否将正方形ABCD划分成有2015个正方形的图形?如果能,请算出是第几次划分,如果不能,需说明理由.
(4)如果设原正方形的边长为1,通过不断地分割该面积为1的正方形,并把数量关系和几何图形巧妙地结合起来,可以很容易得到一些计算结果,试着探究求出下面表达式的结果吧.
计算 ![]() .( 直接写出答案即可)
.( 直接写出答案即可)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com